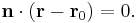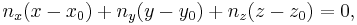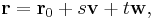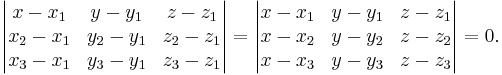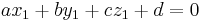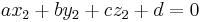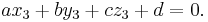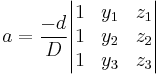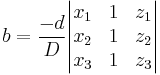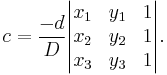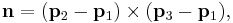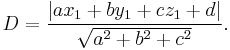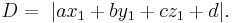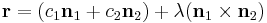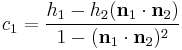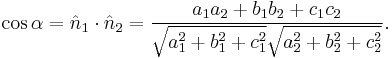Plane (geometry)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point (zero-dimensions), a line (one-dimension) and a space (three-dimensions). Planes can arise as subspaces of some higher dimensional space, as with the walls of a room, or they may enjoy an independent existence in their own right, as in the setting of Euclidean geometry.
When working in two-dimensional Euclidean space, the definite article is used, the plane, to refer to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory and graphing are performed in two-dimensional space, or in other words, in the plane.
Contents
|
Euclidean geometry
Euclid set forth the first known axiomatic treatment of geometry. He selected a small core of undefined terms (called common notions) and postulates (or axioms) which he then used to prove various geometrical statements. Although the plane in its modern sense is not directly given a definition anywhere in the Elements, it may be thought of as part of the common notions.[1] In his work Euclid never makes use of numbers to measure length, angle, or area. In this way the Euclidean plane is not quite the same as the Cartesian plane.
Planes embedded in ℝ3
This section is specifically concerned with planes embedded in three dimensions: specifically, in ℝ3.
Properties
In three-dimensional Euclidean space, we may exploit the following facts that do not hold in higher dimensions:
- Two planes are either parallel or they intersect in a line.
- A line is either parallel to a plane, intersects it at a single point, or is contained in the plane.
- Two lines perpendicular to the same plane must be parallel to each other.
- Two planes perpendicular to the same line must be parallel to each other.
Definition with a point and a normal vector
In a three-dimensional space, another important way of defining a plane is by specifying a point and a normal vector to the plane.
Let r0 be the position vector of some known point 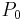 in the plane, and let n be a nonzero vector normal to the plane. The idea is that a point P with position vector r is in the plane if and only if the vector drawn from
in the plane, and let n be a nonzero vector normal to the plane. The idea is that a point P with position vector r is in the plane if and only if the vector drawn from  to P is perpendicular to n. Recalling that two vectors are perpendicular if and only if their dot product is zero, it follows that the desired plane can be expressed as the set of all points r such that
to P is perpendicular to n. Recalling that two vectors are perpendicular if and only if their dot product is zero, it follows that the desired plane can be expressed as the set of all points r such that
(The dot here means a dot product, not scalar multiplication.) Expanded this becomes
which is the familiar equation for a plane.[2]
Defining a plane with a point and two vectors lying on it
Alternatively, a plane may be described parametrically as the set of all points of the form
where s and t range over all real numbers, v and w are given vectors defining the plane, and r0 is the vector representing the position of an arbitrary (but fixed) point on the plane. The vectors v and w can be visualized as vectors starting at r0 and pointing in different directions along the plane. Note that v and w can be perpendicular, but cannot be parallel.
Defining a plane through three points
Let p1=(x1, y1, z1), p2=(x2, y2, z2), and p3=(x3, y3, z3) be non-colinear points.
Method 1
The plane passing through p1, p2, and p3 can be defined as the set of all points (x,y,z) that satisfy the following determinant equations:
Method 2
To describe the plane as an equation in the form 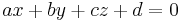 , solve the following system of equations:
, solve the following system of equations:
This system can be solved using Cramer's Rule and basic matrix manipulations. Let
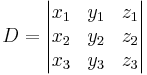 .
.
If D is non-zero (so for planes not through the origin) the values for a, b and c can be calculated as follows:
These equations are parametric in d. Setting d equal to any non-zero number and substituting it into these equations will yield one solution set.
Method 3
This plane can also be described by the "point and a normal vector" prescription above. A suitable normal vector is given by the cross product
and the point r0 can be taken to be any of the given points p1,p2 or p3.[3]
Distance from a point to a plane
For a plane 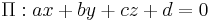 and a point
and a point 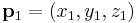 not necessarily lying on the plane, the shortest distance from
not necessarily lying on the plane, the shortest distance from 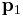 to the plane is
to the plane is
It follows that 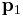 lies in the plane if and only if D=0.
lies in the plane if and only if D=0.
If 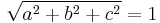 meaning that a, b, and c are normalized then the equation becomes
meaning that a, b, and c are normalized then the equation becomes
Line of intersection between two planes
The line of intersection between two planes 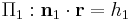 and
and 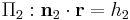 where
where 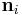 are normalized is given by
are normalized is given by
where
This is found by noticing that the line must be perpendicular to both plane normals, and so parallel to their cross product 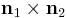 (this cross product is zero if and only if the planes are parallel, and are therefore non-intersecting or entirely coincident).
(this cross product is zero if and only if the planes are parallel, and are therefore non-intersecting or entirely coincident).
The remainder of the expression is arrived at by finding an arbitrary point on the line. To do so, consider that any point in space may be written as 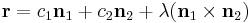 , since
, since 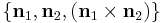 is a basis. We wish to find a point which is on both planes (i.e. on their intersection), so insert this equation into each of the equations of the planes to get two simultaneous equations which can be solved for
is a basis. We wish to find a point which is on both planes (i.e. on their intersection), so insert this equation into each of the equations of the planes to get two simultaneous equations which can be solved for 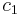 and
and 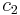 .
.
If we further assume that 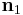 and
and 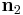 are orthonormal then the closest point on the line of intersection to the origin is
are orthonormal then the closest point on the line of intersection to the origin is 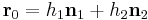 . If that is not the case, then a more complex procedure must be used [1].
. If that is not the case, then a more complex procedure must be used [1].
Dihedral angle
Given two intersecting planes described by 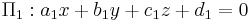 and
and 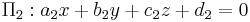 , the dihedral angle between them is defined to be the angle
, the dihedral angle between them is defined to be the angle  between their normal directions:
between their normal directions:
Planes in various areas of mathematics
In addition to its familiar geometric structure, with isomorphisms that are isometries with respect to the usual inner product, the plane may be viewed at various other levels of abstraction. Each level of abstraction corresponds to a specific category.
At one extreme, all geometrical and metric concepts may be dropped to leave the topological plane, which may be thought of as an idealized homotopically trivial infinite rubber sheet, which retains a notion of proximity, but has no distances. The topological plane has a concept of a linear path, but no concept of a straight line. The topological plane, or its equivalent the open disc, is the basic topological neighborhood used to construct surfaces (or 2-manifolds) classified in low-dimensional topology. Isomorphisms of the topological plane are all continuous bijections. The topological plane is the natural context for the branch of graph theory that deals with planar graphs, and results such as the four color theorem.
The plane may also be viewed as an affine space, whose isomorphisms are combinations of translations and non-singular linear maps. From this viewpoint there are no distances, but collinearity and ratios of distances on any line are preserved.
Differential geometry views a plane as a 2-dimensional real manifold, a topological plane which is provided with a differential structure. Again in this case, there is no notion of distance, but there is now a concept of smoothness of maps, for example a differentiable or smooth path (depending on the type of differential structure applied). The isomorphisms in this case are bijections with the chosen degree of differentiability.
In the opposite direction of abstraction, we may apply a compatible field structure to the geometric plane, giving rise to the complex plane and the major area of complex analysis. The complex field has only two isomorphisms that leave the real line fixed, the identity and conjugation.
In the same way as in the real case, the plane may also be viewed as the simplest, one-dimensional (over the complex numbers) complex manifold, sometimes called the complex line. However, this viewpoint contrasts sharply with the case of the plane as a 2-dimensional real manifold. The isomorphisms are all conformal bijections of the complex plane, but the only possibilities are maps that correspond to the composition of a multiplication by a complex number and a translation.
In addition, the Euclidean geometry (which has zero curvature everywhere) is not the only geometry that the plane may have. The plane may be given a spherical geometry by using the stereographic projection. This can be thought of as placing a sphere on the plane (just like a ball on the floor), removing the top point, and projecting the sphere onto the plane from this point). This is one of the projections that may be used in making a flat map of part of the Earth's surface. The resulting geometry has constant positive curvature.
Alternatively, the plane can also be given a metric which gives it constant negative curvature giving the hyperbolic plane. The latter possibility finds an application in the theory of special relativity in the simplified case where there are two spatial dimensions and one time dimension. (The hyperbolic plane is a timelike hypersurface in three-dimensional Minkowski space.)
Topological and differential geometric notions
The one-point compactification of the plane is homeomorphic to a sphere (see stereographic projection); the open disk is homeomorphic to a sphere with the "north pole" missing; adding that point completes the (compact) sphere. The result of this compactification is a manifold referred to as the Riemann sphere or the complex projective line. The projection from the Euclidean plane to a sphere without a point is a diffeomorphism and even a conformal map.
The plane itself is homeomorphic (and diffeomorphic) to an open disk. For the Lobachevsky plane such diffeomorphism is conformal, but for the Euclidean plane it is not.
See also
- Half-plane
- Hyperplane
- Line-plane intersection
- Plane of rotation
- Point on plane closest to origin
- Projective plane
References
- ^ Joyce, D. E. (1996), Euclid's Elements, Book I, Definition 7, Clark University, http://aleph0.clarku.edu/~djoyce/java/elements/bookI/defI7.html, retrieved 8 August 2009
- ^ a b Plane, 2009 of Planes, http://tutorial.math.lamar.edu/Classes/CalcIII/EqnsOfPlanes.aspx
- ^ Dawkins, Paul, "Equations of Planes", Calculus III, http://tutorial.math.lamar.edu/Classes/CalcIII/EqnsOfPlanes.aspx
External links
- The distance from a point to a plane from www.nabla.hr
- Weisstein, Eric W., "Plane" from MathWorld.
- Polygons & the Plane Equation archived from the original on 2009-03-27