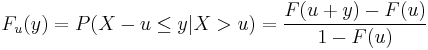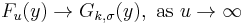Pickands–Balkema–de Haan theorem

The Pickands–Balkema–de Haan theorem is often called the second theorem in extreme value theory. It gives the asymptotic tail distribution of a random variable X, when the true distribution F of X is unknown. Unlike the first theorem (the Fisher–Tippett–Gnedenko theorem) in extreme value theory, the interest here is the values above a threshold.

1 Conditional excess distribution function
2 Statement
3 Special cases of generalized Pareto distribution
4 References

Conditional excess distribution function

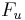If we consider an unknown distribution function $F$ of a random variable $X$ , we are interested in estimating the distribution function $F_u$ of variable $X$ above a certain threshold $u$ . The distribution function F_u is so called the conditional excess distribution function and is defined as

$F_u(y) = P(X-u \leq y | X>u) = \frac{F(u%2By)-F(u)}{1-F(u)} \,$

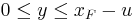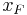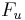for $0 \leq y \leq x_F-u$ , where $x_F$ is either the finite or infinite right endpoint of the underlying distribution $F$ . The function $F_u$ describes the distribution of the excess value over the threshold $u$ , given that $u$ is exceeded.

Statement

Let 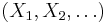$(X_1,X_2,\ldots)$ be a sequence of independent and identically-distributed random variables, let 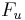$F_u$ be the conditional excess distribution function. Pickands (1975), Balkema and de Haan (1974) posed that for a large class of underlying distribution function F, for u large, F_u is well approximated by the generalized Pareto distribution. That is:

$F_u(y) \rightarrow G_{k, \sigma} (y),\text{ as }u \rightarrow \infty$

where

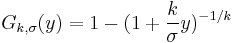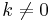
$G_{k, \sigma} (y)= 1-(1%2B\frac{k}{\sigma} y)^{-1/k}$ , if $k \neq 0$
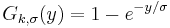$G_{k, \sigma} (y)= 1-e^{-y/\sigma}$ , if $k = 0.$

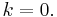
Here σ > 0, and y ≥ 0 when k ≥ 0 and 0 ≤ y ≤ −σ/k when k < 0.

Special cases of generalized Pareto distribution

Exponential distribution with mean $\sigma$ , if k = 0.
Triangular distribution, if k = 1/2.
Uniform distribution on $[0,\sigma]$ , if k = 1.
Pareto distribution, if k < 0.

References

Balkema, A., and Laurens de Haan (1974). "Residual life time at great age", Annals of Probability, 2, 792–804.
Pickands, J. (1975). "Statistical inference using extreme order statistics", Annals of Statistics, 3, 119–131.

Pickands–Balkema–de Haan theorem

Contents

Conditional excess distribution function

Statement

Special cases of generalized Pareto distribution

References