Permutation polynomial

In mathematics, a permutation polynomial (for a given finite ring) is a polynomial that acts as a permutation of the elements of the ring, i.e. the map 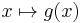$x \mapsto g(x)$ is one-to-one. In case the ring is a finite field, they are (under certain assumptions) essentially Dickson polynomials which are closely related to the Chebyshev polynomials.

In the case of finite rings Z/nZ, such polynomials have also been studied and applied in the interleaver component of error detection and correction algorithms.^[1] ^[2]

1 Quadratic permutation polynomials (QPP)
2 References
- 2.1 Inline

Quadratic permutation polynomials (QPP)

For the finite ring Z/nZ one can construct quadratic permutation polynomials. Actually it is possible if and only if n is divisible by p² for some prime number p. The construction is surprisingly simple, nevertheless it can produce permutations with certain good properties. That is why it has been used in the interleaver component of turbo codes in 3GPP Long Term Evolution mobile telecommunication standard (see 3GPP technical specification 36.212 ^[3] e.g. page 14 in version 8.8.0).

Simple examples

Consider 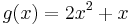$g(x) = 2x^2%2Bx$ for the ring Z/4Z. One sees: 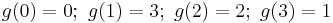$g(0) = 0;~ g(1) = 3;~ g(2) = 2;~ g(3) = 1$ , so the polynomial defines the permutation

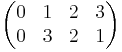$\begin{pmatrix} 0 &1 & 2 & 3 \\ 0 &3 & 2 & 1\end{pmatrix}$ .

Let us consider the same polynomial 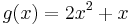$g(x) = 2x^2%2Bx$ for the other ring Z/8Z. One sees: 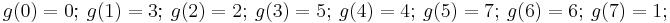$g(0) = 0;~ g(1) = 3;~ g(2) = 2;~ g(3) = 5;~ g(4) = 4;~ g(5) = 7; ~ g(6) = 6; ~ g(7) = 1;$ , so the polynomial defines the permutation

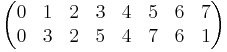$\begin{pmatrix} 0 &1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 0 &3 & 2 & 5 & 4 & 7 & 6 & 1 \end{pmatrix}$ .

Rings Z/p^kZ

Consider 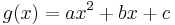$g(x) = ax^2%2Bbx%2Bc$ for the ring Z/p^kZ.

Lemma: for k=1 (i.e. Z/pZ) such polynomial defines a permutation only in the case a=0 and b not equal to zero. So the polynomial is not quadratic, but linear.

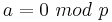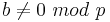Lemma: for k>1 ( Z/p^kZ) such polynomial defines a permutation if and only if $a = 0~ mod~ p$ and $b \ne 0~ mod~ p$ .

Rings Z/nZ

Consider 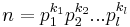$n=p_1^{k_1}p_2^{k_2}...p_l^{k_l}$ , where p_t are prime numbers.

Lemma: any polynomial 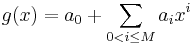$g(x) = a_0%2B \sum_{0<i \le M} a_i x^i$ defines a permutation for the ring Z/nZ if and only if all the polynomials 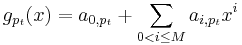$g_{p_t}(x) = a_{0,p_t}%2B \sum_{0<i \le M} a_{i,p_t} x^i$ defines the permutations for all rings 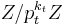$Z/p_t^{k_t}Z$ , where 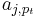$a_{j,p_t}$ are remainders of 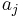$a_{j}$ modula $p_t^{k_t}$ .

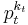As a corollary one can construct plenty quadratic permutation polynomials using the following simple construction. Consider 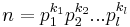$n=p_1^{k_1}p_2^{k_2}...p_l^{k_l}$ , assume that k₁ >1.

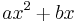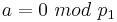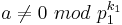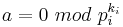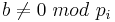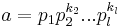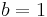Consider $ax^2%2Bbx$ , such that $a= 0~ mod~ p_1$ , but $a\ne 0~ mod~ p_1^{k_1}$ ; assume that $a= 0~ mod~ p_i^{k_i}$ ,i>1. And assume that $b\ne 0~ mod~ p_i$ for all i=1...l. (For example one can take $a=p_1 p_2^{k_2}...p_l^{k_l}$ and $b=1$ ). Then such polynomial defines a permutation.

To see this we observe that for all primes p_i,i>1, the reduction of this quadratic polynomial modula p_i is actually linear polynomial and hence is permutation by trivial reason. For the first prime number we should use the lemma discussed previously to see that it defines the permutation.

For example, consider Z/12Z and polynomial 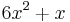$6x^2%2Bx$ . It defines a permutation

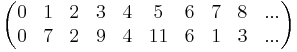$\begin{pmatrix} 0 &1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & ... \\ 0 &7 & 2 & 9 & 4 & 11 & 6 & 1 & 3 & ... \end{pmatrix}$ .

Higher degree polynomials

Consider polynomial 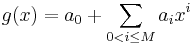$g(x) = a_0%2B \sum_{0<i \le M} a_i x^i$ for the ring Z/p^kZ. In the same way as for quadratic polynomials one can see:

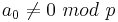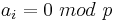Lemma: if $a_0 \ne 0~ mod~ p$ and $a_i = 0~ mod~ p$ i>0, then polynomial g(x) defines a permutation for the elements of the ring Z/p^kZ for k>1.

However contrary to the case of the quadratic polynomials the lemma is not if and only if. This can be seen from the following statement.

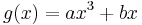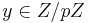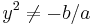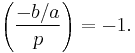Lemma: consider finite field Z/pZ for some prime number p. The cubic polynomial $g(x) = ax^3%2Bbx$ defines a permutation if and only if for all $y \in Z/pZ$ it is true that $y^2\ne -b/a$ , i.e. the Legendre symbol $\left(\frac{-b/a}{p}\right)=-1.$ .

Evaluation of the Legendre symbol can be achieved with the help of quadratic reciprocity law.

So one can see that the analysis of higher degree polynomials to define a permutation is quite subtle question.

References

Inline

^ Takeshita, Oscar (2006). "Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective". arXiv:cs/0601048.
^ Takeshita, Oscar (2005). "A New Construction for LDPC Codes using Permutation Polynomials over Integer Rings". arXiv:cs/0506091.
^ 3GPP TS 36.212