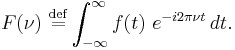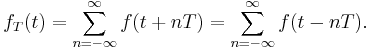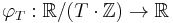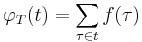Periodic summation
In signal processing, any periodic function 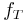 with period
with period 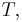 can be represented by a summation of an infinite number of instances of an aperiodic function,
can be represented by a summation of an infinite number of instances of an aperiodic function, 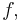 that are offset by integer multiples of
that are offset by integer multiples of 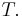 This representation is called periodic summation:
This representation is called periodic summation:
When 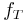 is alternatively represented as a complex Fourier series, the Fourier coefficients are proportional to the values (or "samples") of the continuous Fourier transform of
is alternatively represented as a complex Fourier series, the Fourier coefficients are proportional to the values (or "samples") of the continuous Fourier transform of  at intervals of
at intervals of 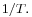 [1] That identity is known as the Poisson summation formula.
[1] That identity is known as the Poisson summation formula.
Quotient space as domain
If a periodic function is represented using the quotient space domain 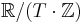 then one can write
then one can write
instead. The arguments of 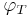 are equivalence classes of real numbers that share the same fractional part when divided by
are equivalence classes of real numbers that share the same fractional part when divided by  .
.
Notes
- ^ The form of the transform assumed here is