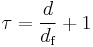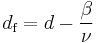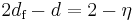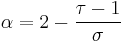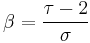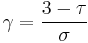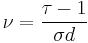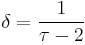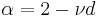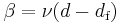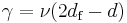Percolation critical exponents

For more information, see Percolation theory.

In the context of percolation theory, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected not to depend on microscopic details like the lattice structure or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.

Percolating systems have a parameter 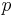p\,\! which controls the occupancy of sites on bonds in the system. At a critical value 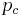p_c\,\!, the mean cluster size goes to infinity and the percolation transition takes place. As one approaches 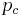p_c\,\!, various quantities either diverge or go to a constant value by a power law in 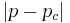|p - p_c|\,\!, and the exponent of that power law is the critical exponent. While the exponent of that power law is generally the same on both sides of the threshold, the coefficient or "amplitude" is generally different, leading to a universal amplitude ratio.

Contents

Description

In the behavior of thermodynamic or configurational systems near a critical point or a continuous phase transition, the system become fractal and the behavior of many quantities are described by universal critical exponents. Percolation theory is a particularly simple and fundamental model in statistical mechanics which has a critical point, and a great deal of work has been done in finding its critical exponents, both theoretically (limited to two dimensions) and numerically.

Critical exponents exist for a variety of observables, but most of them are linked to each other by exponent (or scaling) relations. Only a few of them are independent, and it is a matter of taste what the fundamental exponents are. One choice is the set 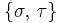\{\sigma,\, \tau\}\,\! motivated by the cluster size distribution, another choice is 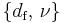\{d_\text{f},\, \nu\}\,\! motivated by the structure of the inifinite cluster. So-called correction exponents extend these sets, they refer to higher orders of the asymptotic expansion around the critical point.

Definitions of exponents

Self-similarity at the percolation threshold

Percolation clusters become self-similar precisely at the threshold density 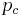p_c\,\! for sufficiently large length scales, entailing the following asymptotic power laws:

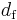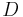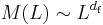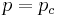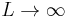The fractal dimension d_\text{f}\,\! or D\,\! relates how the mass of the incipient infinite cluster depends on the radius or another length measure, M(L) \sim L^{d_\text{f}}\,\! at p=p_c\,\! and for large probe sizes, L\to\infty\,\!.

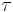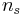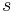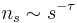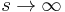The Fisher exponent \tau\,\! characterizes the cluster-size distribution n_s\,\!, which is often determined in computer simulations. The latter counts the number of clusters with a given size (volume) s\,\!, normalized by the total volume (number of lattice sites). The distribution obeys a power law at the threshold, n_s \sim s^{-\tau}\,\! asymptotically as s\to\infty\,\!.

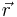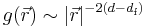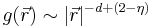The probability for two sites separated by a distance \vec r\,\! to belong to the same cluster decays as g(\vec r)\sim |\vec r|^{-2(d-d_\text{f})}\,\! or g(\vec r)\sim |\vec r|^{-d%2B(2-\eta)}\,\! for large distances, which introduces the anomalous dimension \eta\,\!.

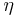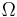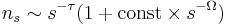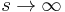The exponent \Omega\,\! is connected with the leading correction to scaling, which appears, e.g., in the asymptotic expansion of the cluster-size distribution, n_s \sim s^{-\tau}(1%2B\text{const} \times s^{-\Omega})\,\! for s\to\infty\,\!.

Critical behavior close to the percolation threshold

The approach to the percolation threshold is governed by power laws again, which hold asymptotically close to 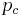p_c\,\!:

The exponent 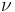\nu\,\! describes the divergence of the correlation length 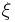\xi\,\! as the percolation transition is approached, 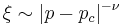\xi \sim |p-p_c|^{-\nu}\,\!. The infinite cluster becomes homogeneous at length scales beyond the correlation length; further, it is a measure for the linear extent of the largest finite cluster.

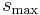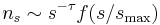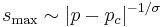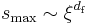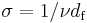Off criticality, only finite clusters exist up to a largest cluster size s_\max\,\!, and the cluster-size distribution is smoothly cut off by a rapidly decaying function, n_s \sim s^{-\tau} f(s/s_\max)\,\!. The exponent \sigma characterizes the divergence of the cutoff parameter, s_\max \sim |p-p_c|^{-1/\sigma}\,\!. Obviously, s_\max \sim \xi^{d_\text{f}}\,\!, yielding \sigma = 1/\nu d_\text{f}\,\!.

The strength or weight of the percolating cluster 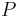P\,\! vanishes at the transition and is non-analytic, 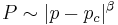P\sim |p-p_c|^\beta\,\!, defining the exponent 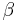\beta\,\!. It plays the role of an order parameter.

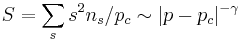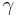The divergence of the mean cluster size S=\sum_s s^2 n_s/p_c \sim |p-p_c|^{-\gamma}\,\! introduces the exponent \gamma\,\!.

Scaling relations

Hyperscaling relations

\tau = \frac{d}{d_\text{f}} %2B 1\,\!
d_\text{f} = d - \frac{\beta}{\nu}\,\!
2 d_\text{f} - d = 2 - \eta\,\!

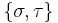
Relations based on \{\sigma, \tau\}

\alpha = 2 - \frac{\tau - 1}{\sigma}\,\!
\beta = \frac{\tau - 2}{\sigma}\,\!
\gamma = \frac{3-\tau}{\sigma}\,\!
\nu = \frac{\tau-1}{\sigma d}\,\!
\delta = \frac{1}{\tau-2}\,\!

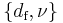
Relations based on \{d_\text{f}, \nu\}

\alpha = 2 - \nu d\,\!
\beta = \nu (d - d_\text{f})\,\!
\gamma = \nu (2 d_\text{f} - d)\,\!
\sigma = 1 / \nu d_\text{f}\,\!

Exponents for standard percolation

d 2 3 4 5 6 – ε
α –2/3 –1 + ε / 7
β 5/36 1 – ε / 7
γ 43/18 1 + ε / 7
η 5/24 0.046(8) [1]*

0.059(9) [2]*

 –ε / 21
ν 4/3 0.875(1) [1]* 1/2 + 5ε / 84
σ 36/91 0.445(10) [1] 1/2 + O(ε²)
τ 187/91 2.186(2) [2]
2.189(2) [1]		 5/2 – 3ε / 14
δ 91/5 5.29(6) [1]
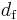d_\text{f} 91/48 2.523(4) [1]*
2.530(4) [2]*
2.5230(1) [3]
2.5226(1) [4]		 4 – 10ε / 21
Ω 0.77(4) [5]
0.77(2) [6]
72/91[7],[8]		 0.64(2) [1]

^* Derived value using the exponent relations above.
The results for the ε-expansion can be found in Ref. [9]

See also

References

  1. ^ a b c d e f g Lorenz, C. D.; R. M. Ziff (1998). "Precise determination of the bond percolation thresholds and finite-size scaling corrections for the sc, fcc, and bcc lattices". Phys. Rev. E 57: 230–236. arXiv:cond-mat/9710044. Bibcode 1998PhRvE..57..230L. doi:10.1103/PhysRevE.57.230. 
  2. ^ a b c Jan, N.; D. Stauffer (1998). "Random Site Percolation in Three Dimensions". Int. J. Mod. Phys. C 9: 341. Bibcode 1998IJMPC...9..341J. doi:10.1142/S0129183198000261. 
  3. ^ Ballesteros, P. N.; L. A. Fernández, V. Martín-Mayor, A. Muñoz, Sudepe, G. Parisi, and J. J. Ruiz-Lorenzo (1999). "Scaling corrections: site percolation and Ising model in three dimensions". Journal of Physics A 32: 1–13. arXiv:cond-mat/9805125. Bibcode 1999JPhA...32....1B. doi:10.1088/0305-4470/32/1/004. 
  4. ^ Deng, Youjin; Henk W. J. Blöte (2005). "Monte Carlo study of the site-percolation model in two and three dimensions". Phys. Rev. E 72: 016126. Bibcode 2005PhRvE..72a6126D. doi:10.1103/PhysRevE.72.016126. 
  5. ^ Kammerer, A.; F. Höfling, T. Franosch (2008). "Cluster-resolved dynamic scaling theory and universal corrections for transport on percolating systems". Europhys. Lett. 84: 66002. Bibcode 2008EL.....8466002K. doi:10.1209/0295-5075/84/66002. 
  6. ^ Ziff, R. M.; F. Babalievski (1999). "Site percolation on the Penrose rhomb lattice". Physica A 269: 201. Bibcode 1999PhyA..269..201Z. doi:10.1016/S0378-4371(99)00166-1. 
  7. ^ Ziff, R. M. (2011). "Correction-to-scaling exponent for two-dimensional percolation". Phys. Rev. E 83 (2): 020107. doi:10.1103/PhysRevE.83.020107. 
  8. ^ Aharony, Amnon; Asikainen, Joonas (2003). "Fractal dimension and corrections to scaling for critical Potts clusters". Fractals, Supplementary Issue 11 (1): 3-7. doi:10.1142/S0218348X03001665. 
  9. ^ Essam, J. W. (1980). "Percolation theory". Rep. Prog. Phys. 43 (7): 833. Bibcode 1980RPPh...43..833E. doi:10.1088/0034-4885/43/7/001. http://stacks.iop.org/0034-4885/43/i=7/a=001. 

Further reading