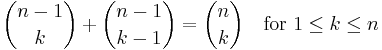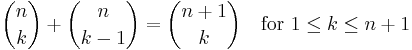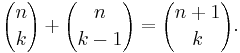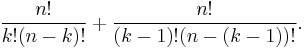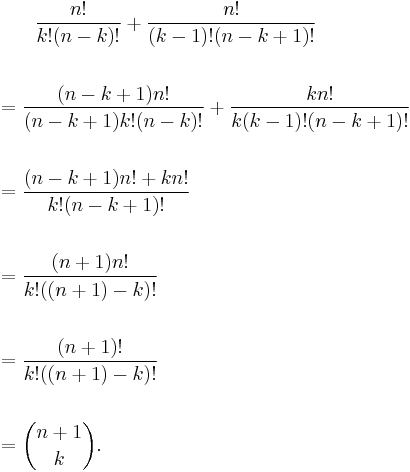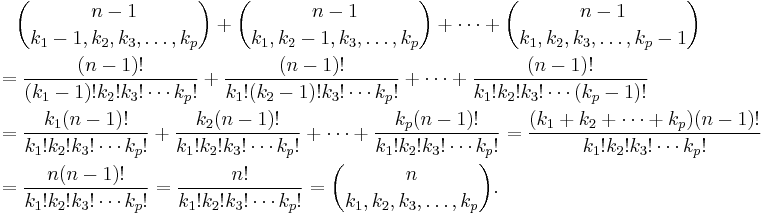Pascal's rule

Not to be confused with Pascal's law.

In mathematics, Pascal's rule is a combinatorial identity about binomial coefficients. It states that for any natural number n we have

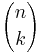{n-1\choose k} %2B {n-1\choose k-1} = {n\choose k}\quad\text{for }1 \le k \le n

where {n\choose k} is a binomial coefficient. This is also commonly written

{n \choose k} %2B {n \choose k-1} = {n %2B 1 \choose k} \quad\text{for } 1 \le k \le n %2B 1

Contents

Combinatorial proof

Pascal's rule has an intuitive combinatorial meaning. Recall that 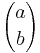{a\choose b} counts in how many ways can we pick a subset with b elements out from a set with a elements. Therefore, the right side of the identity 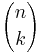{n\choose k} is counting how many ways can we get a k-subset out from a set with n elements.

Now, suppose you distinguish a particular element 'X' from the set with n elements. Thus, every time you choose k elements to form a subset there are two possibilities: X belongs to the chosen subset or not.

If X is in the subset, you only really need to choose k − 1 more objects (since it is known that X will be in the subset) out from the remaining n − 1 objects. This can be accomplished in 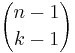n-1\choose k-1 ways.

When X is not in the subset, you need to choose all the k elements in the subset from the n − 1 objects that are not X. This can be done in 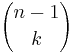n-1\choose k ways.

We conclude that the numbers of ways to get a k-subset from the n-set, which we know is 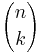{n\choose k}, is also the number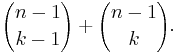 {n-1\choose k-1} %2B {n-1\choose k}.

See also Bijective proof.

Algebraic proof

We need to show

{ n \choose k } %2B { n \choose k-1 } = { n%2B1 \choose k }.

Let us begin by writing the left-hand side as

\frac{n!}{k!(n-k)!} %2B \frac{n!}{(k-1)!(n-(k-1))!}.

Getting a common denominator and simplifying, we have

\begin{align} & {} \qquad \frac{n!}{k!(n-k)!} %2B \frac{n!}{(k-1)!(n-k%2B1)!} \\\\ & = \frac{(n-k%2B1)n!}{(n-k%2B1)k!(n-k)!}%2B\frac{kn!}{k(k-1)!(n-k%2B1)!} \\\\ & = \frac{(n-k%2B1)n!%2Bkn!}{k!(n-k%2B1)!} \\\\ & = \frac{(n%2B1)n!}{k!((n%2B1)-k)!} \\\\ & = \frac{(n%2B1)!}{k!((n%2B1)-k)!} \\\\ & = { n%2B1 \choose k }. \end{align}

Generalization

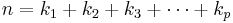Let n, k_1, k_2, k_3,\dots ,k_p, p \in \mathbb{N}^* \,\! and n=k_1%2Bk_2%2Bk_3%2B \cdots %2Bk_p \,\!. Then

\begin{align} & {} \quad {n-1\choose k_1-1,k_2,k_3, \dots, k_p}%2B{n-1\choose k_1,k_2-1,k_3,\dots, k_p}%2B\cdots%2B{n-1\choose k_1,k_2,k_3,\dots,k_p-1} \\ & = \frac{(n-1)!}{(k_1-1)!k_2!k_3! \cdots k_p!} %2B \frac{(n-1)!}{k_1!(k_2-1)!k_3!\cdots k_p!} %2B \cdots %2B \frac{(n-1)!}{k_1!k_2!k_3! \cdots (k_p-1)!} \\ & = \frac{k_1(n-1)!}{k_1!k_2!k_3! \cdots k_p!} %2B \frac{k_2(n-1)!}{k_1!k_2!k_3! \cdots k_p!} %2B \cdots %2B \frac{k_p(n-1)!}{k_1!k_2!k_3! \cdots k_p!} = \frac{(k_1%2Bk_2%2B\cdots%2Bk_p) (n-1)!}{k_1!k_2!k_3!\cdots k_p!} \\ & = \frac{n(n-1)!}{k_1!k_2!k_3! \cdots k_p!} = \frac{n!}{k_1!k_2!k_3! \cdots k_p!} = {n\choose k_1, k_2, k_3, \dots , k_p}. \end{align}

See also

Sources

External links