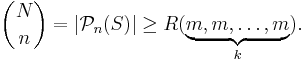Paris–Harrington theorem
In mathematical logic, the Paris–Harrington theorem states that a certain combinatorial principle in Ramsey theory is true, but not provable in Peano arithmetic. This was the first "natural" example of a true statement about the integers that could be stated in the language of arithmetic, but not proved in Peano arithmetic; it was already known that such statements existed by Gödel's first incompleteness theorem.
Contents |
The strengthened finite Ramsey theorem
The strengthened finite Ramsey theorem is a statement about colorings and natural numbers. (It should not be confused with the Paris–Harrington theorem, which is a statement about the strengthened finite Ramsey theorem, namely, that the strengthened Ramsey theorem is not provable in Peano arithmetic.) This theorem states that:
- For any positive integers n, k, m we can find N with the following property: if we color each of the n-element subsets of S = {1, 2, 3,..., N} with one of k colors, then we can find a subset Y of S with at least m elements, such that all n element subsets of Y have the same color, and the number of elements of Y is at least the smallest element of Y.
Without the condition that the number of elements of Y is at least the smallest element of Y, this is a corollary the statement of the finite Ramsey theorem in 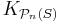 , with N given by:
, with N given by:
Moreover the strengthened finite Ramsey theorem can be deduced from the infinite Ramsey theorem in almost exactly the same way that the finite Ramsey theorem can be deduced from it, using a compactness argument (see the article on Ramsey's theorem for details). This proof can be carried out in second-order arithmetic.
The Paris–Harrington theorem
Roughly speaking, Jeff Paris and Leo Harrington showed that the strengthened finite Ramsey theorem is unprovable in Peano arithmetic by showing that (in Peano arithmetic) it implies the consistency of Peano arithmetic. Since Peano arithmetic cannot prove its own consistency by Gödel's theorem, this shows that Peano arithmetic cannot prove the strengthened finite Ramsey theorem.
The smallest number N that satisfies the strengthened finite Ramsey theorem is a computable function of n, m, k, but grows extremely fast. In particular it is not primitive recursive, but it is also far larger than standard examples of non primitive recursive functions such as the Ackermann function. Its growth is so large that Peano arithmetic cannot prove it is defined everywhere, although Peano arithmetic easily proves that the Ackermann function is well defined.
See also
References
- David Marker, Model Theory: An Introduction, ISBN 0387987606
- mathworld entry
- Paris, J. and Harrington, L. A Mathematical Incompleteness in Peano Arithmetic. In Handbook for Mathematical Logic (Ed. J. Barwise). Amsterdam, Netherlands: North-Holland, 1977.
External links
- A brief introduction to unprovability (contains a proof of the Paris-Harrington theorem) by Andrey Bovykin.