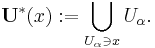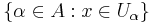Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by Dieudonné (1944).
Contents |
Definitions of relevant terms
- A cover of a set X is a collection of subsets of X whose union is X. In symbols, if U = {Uα : α in A} is an indexed family of subsets of X, then U is a cover if and only if
- A cover of a topological space X is open if all its members are open sets. In symbols, a cover U is an open cover if U is a subset of T, where T is the topology on X.
- A refinement of a cover of a space X is a new cover of the same space such that every set in the new cover is a subset of some set in the old cover. In symbols, the cover V = {Vβ : β in B} is a refinement of the cover U = {Uα : α in A} if and only if, for any Vβ in V, there exists some Uα in U such that Vβ is contained in Uα.
- An open cover of a space X is locally finite if every point of the space has a neighborhood which intersects only finitely many sets in the cover. In symbols, U = {Uα : α in A} is locally finite if and only if, for any x in X, there exists some neighbourhood V(x) of x such that the set
- is finite.
- A topological space X is called paracompact if any open cover of X admits an open refinement that is locally finite.
Note the similarity between the definitions of compact and paracompact: for paracompact, we replace "subcover" by "open refinement" and "finite" by "locally finite". Both of these changes are significant: if we take the above definition of paracompact and change "open refinement" back to "subcover", or "locally finite" back to "finite", we end up with the compact spaces in both cases.
A hereditarily paracompact space is a space such that every subspace of it is paracompact. This is equivalent to requiring that every open subspace be paracompact.
Examples and counterexamples
- Every compact space is paracompact.
- (Theorem of A. H. Stone) Every metric space is paracompact. Early proofs were somewhat involved, but an elementary one was found by M. E. Rudin.[1] Existing proofs of this require the axiom of choice for the non-separable case. It has been shown that neither ZF theory nor ZF theory with the axiom of dependent choice is sufficient.[2]
- Every regular Lindelöf space is paracompact. In particular, every locally compact Hausdorff second-countable space is paracompact.
- The Sorgenfrey line is paracompact, even though it is neither compact, locally compact, second countable, nor metrizable.
- Every CW complex is paracompact [3]
Some examples of spaces that are not paracompact include:
- The most famous counterexample is the long line, which is a nonparacompact topological manifold. (The long line is locally compact, but not second countable.)
- Another counterexample is a product of uncountably many copies of an infinite discrete space. Any infinite set carrying the particular point topology is not paracompact; in fact it is not even metacompact.
- The Prüfer manifold is a non-paracompact surface.
Properties
- (Theorem of Jean Dieudonné) Every paracompact Hausdorff space is normal.
- Paracompactness is weakly hereditary, i.e. every closed subspace of a paracompact space is paracompact. This can be extended to F-sigma subspaces as well.
- If every open subset of a space is paracompact, then it is hereditarily paracompact.
- A regular space is paracompact if every open cover admits a locally finite refinement. (Here, the refinement is not required to be open.) In particular, every regular Lindelof space is paracompact.
- (Smirnov metrization theorem) A topological space is metrizable if and only if it is paracompact, Hausdorff, and locally metrizable.
- Every paracompact Hausdorff space is a shrinking space, that is, every open cover of a paracompact Hausdorff space has a shrinking: another open cover indexed by the same set such that the closure of every set in the new cover lies inside the corresponding set in the old cover.
- On paracompact Hausdorff spaces, the cohomology of a sheaf is equal to its Čech cohomology.
- Michael selection theorem states that lower semicontinuous multifunctions from X into nonempty closed convex subsets of Banach spaces admit continuous selection iff X is paracompact.
Partitions of unity
Paracompactness has little to do with the notion of compactness, but rather more to do with breaking up topological space entities into manageable pieces. The most important feature of paracompact Hausdorff spaces is that they are normal and admit partitions of unity subordinate to any open cover. This means the following: if X is a paracompact Hausdorff space with a given open cover, then there exists a collection of continuous functions on X with values in the unit interval [0, 1] such that:
- for every function f: X → R from the collection, there is an open set U from the cover such that the support of f is contained in U;
- for every point x in X, there is a neighborhood V of x such that all but finitely many of the functions in the collection are identically 0 in V and the sum of the nonzero functions is identically 1 in V.
In fact, a Hausdorff space is paracompact if and only if it admits partitions of unity subordinate to any open cover (see below). This property is sometimes used to define paracompact spaces (at least in the Hausdorff case).
Partitions of unity are useful because they often allow one to extend local constructions to the whole space. For instance, the integral of differential forms on paracompact manifolds is first defined locally (where the manifold looks like Euclidean space and the integral is well known), and this definition is then extended to the whole space via a partition of unity.
Proof that paracompact hausdorff spaces admit partitions of unity
An hausdorff space 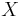 is paracompact if and only if it every open cover admits a subordinate partition of unity. The if direction is straightforward. Now for the only if direction, we do this in a few stages.
is paracompact if and only if it every open cover admits a subordinate partition of unity. The if direction is straightforward. Now for the only if direction, we do this in a few stages.
- Lemma 1: If
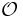 is a locally finite open cover, then there exists open sets
is a locally finite open cover, then there exists open sets 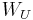 for each
for each 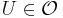 , such that each
, such that each 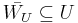 and
and 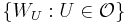 is a locally finite refinement.
is a locally finite refinement.
- Lemma 2: If
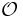 is a locally finite open cover, then there are continuous functions
is a locally finite open cover, then there are continuous functions ![f_{U}:X\to[0,1]\,](/2012-wikipedia_en_all_nopic_01_2012/I/f4457659af52341d11b154b0b9915543.png) such that
such that 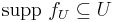 and such that
and such that 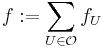 is a continuous function which is always non-zero and finite.
is a continuous function which is always non-zero and finite.
- Theorem: In a paracompact hausdorff space
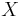 , if
, if 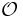 is an open cover, then there exists a partition of unity subordinate to it.
is an open cover, then there exists a partition of unity subordinate to it.
- Proof (Lemma 1): Let
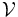 be the collection of open sets meeting only finitely many sets in
be the collection of open sets meeting only finitely many sets in 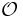 , and whose closure is contained in a set in
, and whose closure is contained in a set in 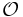 . One can check as an exercise that this provides an open refinement, since paracompact hausdorff spaces are regular, and since
. One can check as an exercise that this provides an open refinement, since paracompact hausdorff spaces are regular, and since 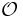 is locally finite. Now replace
is locally finite. Now replace 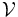 by a locally finite open refinitement. One can easily check that each set in this refinement has the same property as that which characterised the original cover.
by a locally finite open refinitement. One can easily check that each set in this refinement has the same property as that which characterised the original cover.
- Now we define
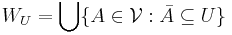 . We have that each
. We have that each 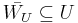 ; for otherwise letting
; for otherwise letting 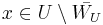 , we take
, we take 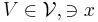 with closure contained in
with closure contained in 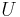 ; but then
; but then 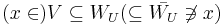 a contradiction. And it easy to see that
a contradiction. And it easy to see that 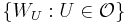 is an open refinement of
is an open refinement of 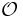 .
.
- Finally, to verify that this cover is locally finite, fix
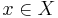 ; let
; let 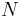 a neighbourhood of
a neighbourhood of 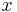 meeting only finitely many sets in
meeting only finitely many sets in 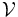 . We will show that
. We will show that  meets only finitely many of the
meets only finitely many of the 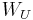 . If
. If 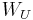 meets
meets 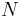 , then some
, then some 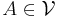 with
with 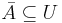 meets
meets 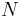 . Thus
. Thus 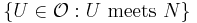 is the same as
is the same as 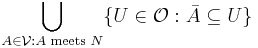 which is contained in
which is contained in 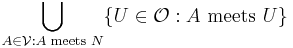 . By the setup of
. By the setup of  , each
, each 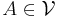 meets only finitely many sets in
meets only finitely many sets in 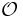 . Hence the right-hand collection is a finite union of finite sets. Thus
. Hence the right-hand collection is a finite union of finite sets. Thus 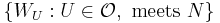 is finite. Hence the cover is locally finite.
is finite. Hence the cover is locally finite.
|
|
- Proof (Lemma 2): Applying Lemma 1, let
![f_{U}:X\to[0,1]\,](/2012-wikipedia_en_all_nopic_01_2012/I/f4457659af52341d11b154b0b9915543.png) be coninuous maps with
be coninuous maps with 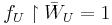 and
and 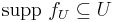 (by Urysohn's lemma for disjoint closed sets in normal spaces, which a paracompact hausdorff space is). Note by the support of a function, we here mean the points not mapping to zero (and not the closure of this set). To show that
(by Urysohn's lemma for disjoint closed sets in normal spaces, which a paracompact hausdorff space is). Note by the support of a function, we here mean the points not mapping to zero (and not the closure of this set). To show that 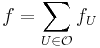 is always finite and non-zero, take
is always finite and non-zero, take 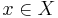 , and let
, and let 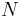 a neighbourhood of
a neighbourhood of 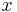 meeting only finitely many sets in
meeting only finitely many sets in 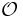 ; thus
; thus 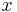 belongs to only finitely many sets in
belongs to only finitely many sets in 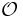 ; thus
; thus 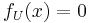 for all but finitely many
for all but finitely many 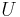 ; moreover
; moreover 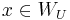 for some
for some 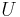 , thus
, thus 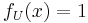 ; so
; so 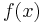 is finite and
is finite and 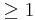 . To establish continuity, take
. To establish continuity, take 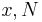 as before, and let
as before, and let 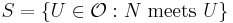 , which is finite; then
, which is finite; then 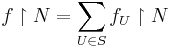 , which is a continuous function; hence the preimage under
, which is a continuous function; hence the preimage under 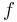 of a neighbourhood of
of a neighbourhood of 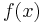 will be a neighbourhood of
will be a neighbourhood of 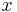 .
.
|
|
- Proof (Theorem): Take
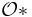 a locally finite subcover of the refinement cover:
a locally finite subcover of the refinement cover: 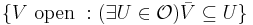 . Applying Lemma 2, we obtain continuous functions
. Applying Lemma 2, we obtain continuous functions ![f_{W}:X\to[0,1]\,](/2012-wikipedia_en_all_nopic_01_2012/I/9be3416ee7a7e88d3bbd72b6bee3ded7.png) with
with 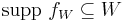 (thus the usual closed version of the support is contained in some
(thus the usual closed version of the support is contained in some 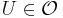 , for each
, for each 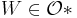 ; for which their sum constitutes a continuous function which is always finite non-zero (hence
; for which their sum constitutes a continuous function which is always finite non-zero (hence 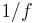 is continuous positive, finite-valued). So replacing each
is continuous positive, finite-valued). So replacing each 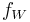 by
by 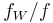 , we have now — all things remaining the same — that their sum is everywhere
, we have now — all things remaining the same — that their sum is everywhere  . Finally for
. Finally for 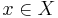 , letting
, letting 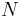 be a neighbourhood of
be a neighbourhood of 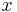 meeting only finitely many sets in
meeting only finitely many sets in 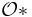 , we have
, we have 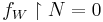 for all but finitely many
for all but finitely many 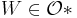 since each
since each 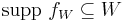 . Thus we have a partition of unity subordinate to the original open cover.
. Thus we have a partition of unity subordinate to the original open cover.
|
|
Comparison with compactness
Paracompactness is similar to compactness in the following respects:
- Every closed subset of a paracompact space is paracompact.
- Every paracompact Hausdorff space is normal.
It is different in these respects:
- A paracompact subset of a Hausdorff space need not be closed. In fact, for metric spaces, all subsets are paracompact.
- A product of paracompact spaces need not be paracompact. The square of the real line R in the lower limit topology is a classical example for this.
Although a product of paracompact spaces need not be paracompact, the following are true:
- The product of a paracompact space and a compact space is paracompact.
- The product of a metacompact space and a compact space is metacompact.
Both these results can be proved by the tube lemma which is used in the proof that a product of finitely many compact spaces is compact.
Variations
There are several variations of the notion of paracompactness. To define them, we first need to extend the list of terms above:
- Given a cover and a point, the star of the point in the cover is the union of all the sets in the cover that contain the point. In symbols, the star of x in U = {Uα : α in A} is
- The notation for the star is not standardised in the literature, and this is just one possibility.
- A star refinement of a cover of a space X is a new cover of the same space such that, given any point in the space, the star of the point in the new cover is a subset of some set in the old cover. In symbols, V is a star refinement of U = {Uα : α in A} if and only if, for any x in X, there exists a Uα in U, such that V*(x) is contained in Uα.
- A cover of a space X is pointwise finite if every point of the space belongs to only finitely many sets in the cover. In symbols, U is pointwise finite if and only if, for any x in X, the set
- is finite.
A topological space is:
- metacompact if every open cover has an open pointwise finite refinement.
- orthocompact if every open cover has an open refinement such that the intersection of all the open sets about any point in this refinement is open.
- fully normal if every open cover has an open star refinement, and fully T4 if it is fully normal and T1 (see separation axioms).
The adverb "countably" can be added to any of the adjectives "paracompact", "metacompact", and "fully normal" to make the requirement apply only to countable open covers.
Every paracompact space is metacompact, and every metacompact space is orthocompact.
As the name implies, a fully normal space is normal. Every fully T4 space is paracompact. In fact, for Hausdorff spaces, paracompactness and full normality are equivalent. Thus, a fully T4 space is the same thing as a paracompact Hausdorff space.
As an historical note: fully normal spaces were defined before paracompact spaces. The proof that all metrizable spaces are fully normal is easy. When it was proved by A.H. Stone that for Hausdorff spaces fully normal and paracompact are equivalent, he implicitly proved that all metrizable spaces are paracompact. Later M.E. Rudin gave a direct proof of the latter fact.
See also
Notes
- ^ Rudin, Mary Ellen. A new proof that metric spaces are paracompact. Proceedings of the American Mathematical Society, Vol. 20, No. 2. (Feb., 1969), p. 603.
- ^ C. Good, I. J. Tree, and W. S. Watson. On Stone's Theorem and the Axiom of Choice. Proceedings of the American Mathematical Society, Vol. 126, No. 4. (April, 1998), pp. 1211–1218.
- ^ Hatcher, Allen, Vector bundles and K-theory, preliminary version available on the authors homepage
References
- Dieudonné, Jean (1944), "Une généralisation des espaces compacts", Journal de Mathématiques Pures et Appliquées. Neuvième Série 23: 65–76, ISSN 0021-7824, MR0013297
- Lynn Arthur Steen and J. Arthur Seebach, Jr., Counterexamples in Topology (2 ed), Springer Verlag, 1978, ISBN 3-540-90312-7. P.23.
- Willard, Stephen (1970). General Topology. Reading, Massachusetts: Addison-Wesley. ISBN 0-486-43479-6 (Dover edition).
- Mathew, Akhil. "Topology/Paracompactness". http://amathew.wordpress.com/2010/08/17/paracompactness/.
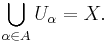
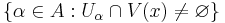
 (Lem 1)
(Lem 1)