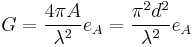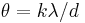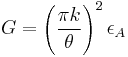Parabolic antenna
A parabolic antenna is an antenna that uses a parabolic reflector, a curved surface with the cross-sectional shape of a parabola, to direct the radio waves. The most common form is shaped like a dish and is popularly called a dish antenna or parabolic dish. The main advantage of a parabolic antenna is that it is highly directive; it functions similarly to a searchlight or flashlight reflector to direct the radio waves in a narrow beam, or receive radio waves from one particular direction only. Parabolic antennas have some of the highest gains, that is they can produce the narrowest beam width angles, of any antenna type.[1] In order to achieve narrow beamwidths, the parabolic reflector must be much larger than the wavelength of the radio waves used, so parabolic antennas are used in the high frequency part of the radio spectrum, at UHF and microwave (SHF) frequencies, at which wavelengths are small enough that conveniently sized dishes can be used.
Parabolic antennas are used as high-gain antennas for point-to-point communication, in applications such as microwave relay links that carry telephone and television signals between nearby cities, wireless WAN/LAN links for data communications, satellite and spacecraft communication antennas, and radio telescopes. Their other large use is in radar antennas, which need to emit a narrow beam of radio waves to locate objects like ships and airplanes. With the advent of home satellite television dishes, parabolic antennas have become a ubiquitous feature of the modern landscape.
Contents |
Design
The operating principle of a parabolic antenna is that a point source of radio waves at the focal point in front of a paraboloidal reflector of conductive material will be reflected into a collimated plane wave beam along the axis of the reflector. Conversely, an incoming plane wave parallel to the axis will be focused to a point at the focal point.
A typical parabolic antenna consists of a metal parabolic reflector with a small feed antenna suspended in front of the reflector at its focus, pointed back toward the reflector. The reflector is a metallic surface formed into a paraboloid of revolution and usually truncated in a circular rim that forms the diameter of the antenna. In a transmitting antenna, radio frequency current from a transmitter is supplied through a transmission line cable to the feed antenna, which converts it into radio waves. The radio waves are emitted back toward the dish by the feed antenna and reflect off the dish into a parallel beam. In a receiving antenna the incoming radio waves bounce off the dish and are focussed to a point at the feed antenna, which converts them to electric currents which travel through a transmission line to the receiver.
Parabolic reflector
The reflector can be of sheet metal, metal screen, or wire grill construction, and it can be either a circular "dish" or various other shapes to create different beam shapes. A metal screen reflects radio waves as well as a solid metal surface as long as the holes are smaller than 1/10 of a wavelength, so screen reflectors are often used to reduce weight and wind loads on the dish. To achieve the maximum gain, it is necessary that the shape of the dish be accurate within a small fraction of a wavelength, to ensure the waves from different parts of the antenna arrive at the focus in phase. Large dishes often require a supporting truss structure behind them to provide the required stiffness.
A reflector made of a grill of parallel wires or bars oriented in one direction acts as a polarizing filter as well as a reflector. It only reflects linearly polarized radio waves, with the electric field parallel to the grill elements. This type is often used in radar antennas. Combined with a linearly polarized feed horn, it helps filter out noise in the receiver and reduces false returns.
Feed antenna
The feed antenna at the reflector's focus is typically a low-gain type such as a half-wave dipole or more often a small horn antenna called a feed horn. In more complex designs, such as the Cassegrain and Gregorian, a secondary reflector is used to direct the energy into the parabolic reflector from a feed antenna located away from the primary focal point. The feed antenna is connected to the associated radio-frequency (RF) transmitting or receiving equipment by means of a coaxial cable transmission line or waveguide.
An advantage of parabolic antennas is that most of the structure of the antenna (all of it except the feed antenna) is nonresonant, so it can function over a wide range of frequencies, that is a wide bandwidth. All that is necessary to change the frequency of operation is to replace the feed antenna with one that works at the new frequency. Some parabolic antennas transmit or receive at multiple frequencies by having several feed antennas mounted at the focal point, close together.
Dish parabolic antennas
Shaped-beam parabolic antennas
Types
Parabolic antennas are distinguished by their shapes:
- Paraboloidal or dish - The reflector is shaped like a paraboloid. This is the most common type. It radiates a narrow pencil-shaped beam along the axis of the dish.
- Shrouded dish - Sometimes a cylindrical metal shield is attached to the rim of the dish.[2] The shroud shields the antenna from radiation from angles outside the main beam axis, reducing the sidelobes. It is sometimes used to prevent interference in terrestrial microwave links, where several antennas using the same frequency are located close together. The shroud is coated inside with microwave absorbent material. Shrouds can reduce back lobe radiation by 10 dB.[2]
- Cylindrical - The reflector is curved in only one direction and flat in the other. The radio waves come to a focus not at a point but along a line. The feed is sometimes a dipole antenna located along the focal line. Cylindrical parabolic antennas radiate a fan-shaped beam, narrow in the curved dimension, and wide in the uncurved dimension. The curved ends of the reflector are sometimes capped by flat plates, to prevent radiation out the ends, and this is called a pillbox antenna.
- Shaped-beam antennas - Modern parabolic antennas can be designed to produce a beam or beams of a particular shape, rather than just a narrow "pencil" beam that simple "dish" emits.[3] Two techniques are used, sometimes in combination, to control the shape of the beam:
- Shaped reflectors - With a single feed antenna, the only option is to alter the shape of the reflector(s). The parabolic reflector can be given a noncircular shape, and/or different curvatures in the horizontal and vertical directions, to alter the shape of the beam. This is often used in radar antennas.
- Arrays of feeds - In order to produce an arbitrary shaped beam, instead of one feed horn an array of feed horns clustered around the focal point can be used. Array-fed antennas are often used on communication satellites, particularly direct broadcast satellites, to limit the downlink radiation pattern to a particular continent or coverage area required.
Parabolic antennas are also classified by the type of feed, that is, how the radio waves are supplied to the antenna:[2]
- Axial or front feed - This is the most common type of feed, with the feed antenna located in front of the dish at the focus, on the beam axis. A disadvantage of this type is that the feed and its supports block some of the beam, which limits the aperture efficiency to only 55 - 60%.[2]
- Offset or off-axis feed - The reflector is an asymmetrical segment of a paraboloid, so the focus, and the feed antenna, are located to one side of the dish. The purpose of this design is to move the feed structure out of the beam path, so it doesn't block the beam. It is widely used in home satellite television dishes, which are small enough that the feed structure would otherwise block a significant percentage of the signal. Offset feed is also used in multiple reflector designs such as the Cassegrain and Gregorian, below.
- Cassegrain - In a Cassegrain antenna the feed is located on or behind the dish, and radiates forward, illuminating a convex hyperboloidal secondary reflector at the focus of the dish. The radio waves from the feed reflect back off the secondary reflector to the dish, which forms the outgoing beam. An advantage of this configuration is that the feed, with its waveguides and "front end" electronics does not have to be suspended in front of the dish, so it is used for antennas with complicated or bulky feeds, such as large satellite communication antennas and radio telescopes. Aperture efficiency is on the order of 65 - 70%[2]
- Gregorian - Similar to the Cassegrain design except that the secondary reflector is concave, (ellipsoidal) in shape. Aperture efficiency over 70% can be achieved.[2]
Feed pattern
The radiation pattern of the feed antenna has to be tailored to the shape of the dish, because it has a strong influence on the aperture efficiency, which determines the antenna gain (see Gain section below). Radiation from the feed that falls outside the edge of the dish is called "spillover" and is wasted, reducing the gain and increasing the backlobes, possibly causing interference or (in receiving antennas) increasing susceptibility to ground noise. However, maximum gain is only achieved when the dish is uniformly "illuminated" with a constant field strength to its edges. So the ideal radiation pattern of a feed antenna would be a constant field strength throughout the solid angle of the dish, dropping abruptly to zero at the edges. However, practical feed antennas have radiation patterns that drop off gradually at the edges, so the feed antenna is a compromise between acceptably low spillover and adequate illumination. For most front feed horns, optimum illumination is achieved when the power radiated by the feed horn is 10 dB less at the dish edge than its maximum value at the center of the dish.[4]
History
The idea of using parabolic reflectors for radio antennas was taken from optics, where the power of a parabolic mirror to focus light into a beam has been known since classical antiquity. The designs of some specific types of parabolic antenna, such as the Cassegrain and Gregorian, come from similarly named analogous types of reflecting telescope, which were invented by astronomers during the 15th century.[5]
German physicist Heinrich Hertz constructed the world's first parabolic reflector antenna in 1888. The antenna was a cylindrical parabolic reflector made of zinc sheet metal supported by a wooden frame, and had a spark-gap excited dipole along the focal line. Its aperture was 2 meters high by 1.2 meters wide, with a focal length of 0.12 meters, and was used at an operating frequency of about 450 MHz. With two such antennas, one used for transmitting and the other for receiving, Hertz demonstrated the existence of radio waves which had been predicted by James Clerk Maxwell some 22 years earlier.[6]
Italian radio pioneer Guglielmo Marconi used a parabolic reflector during the 1930s in investigations of UHF transmission from his boat in the Mediterranean.[5] In 1931 a microwave relay link across the English Channel using 10 ft. (3 meter) diameter dishes was demonstrated.[5] In 1937 Grote Reber built the first radio telescope to use a parabolic antenna and did a sky survey with it, one of the events that founded the field of radio astronomy.[5] The development of radar during World War II provided a great impetus to parabolic antenna research, and saw the evolution of shaped-beam antennas, in which the curve of the reflector is different in the vertical and horizontal directions, tailored to produce a beam with a particular shape.[5] During the 1950s dish antennas became widely used in terrestrial microwave relay communication systems.[5]
The first parabolic antenna used for satellite communications was constructed in 1962 at Goonhilly in Cornwall, England, UK to communicate with the Telstar satellite.
Gain
The directive qualities of an antenna are measured by a dimensionless parameter called its gain, which is the ratio of the power received by the antenna from a source along its beam axis to the power received by a hypothetical isotropic antenna. The gain of a parabolic antenna is:[8]
where:
 is the area of the antenna aperture, that is, the mouth of the parabolic reflector
is the area of the antenna aperture, that is, the mouth of the parabolic reflector is the diameter of the parabolic reflector
is the diameter of the parabolic reflector is the wavelength of the radio waves.
is the wavelength of the radio waves.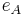 is a dimensionless parameter between 0 and 1 called the aperture efficiency. The aperture efficiency of typical parabolic antennas is 0.55 to 0.70.
is a dimensionless parameter between 0 and 1 called the aperture efficiency. The aperture efficiency of typical parabolic antennas is 0.55 to 0.70.
It can be seen that, as with any aperture antenna, the larger the aperture is, compared to the wavelength, the higher the gain. The gain increases with the square of the ratio of aperture width to wavelength, so large parabolic antennas, such as those used for spacecraft communication and radio telescopes, can have extremely high gain. Applying the above formula to the 25-meter-diameter antennas used by the VLA and VLBA radio telescopes at a wavelength of 21 cm (1.42 GHz, a common radio astronomy frequency) yields an approximate maximum gain of 140,000 times or about 50 dBi (decibels above the isotropic level).
Aperture efficiency eA is a catchall variable which accounts for various losses that reduce the gain of the antenna from the maximum that could be achieved with the given aperture. The major factors reducing the aperture efficiency in parabolic antennas are:.[9]
- Feed spillover - Some of the radiation from the feed antenna falls outside the edge of the dish and so doesn't contribute to the main beam.
- Feed illumination taper - The maximum gain for any aperture antenna is only achieved when the intensity of the radiated beam is constant across the entire aperture area. However the radiation pattern from the feed antenna usually tapers off toward the outer part of the dish, so the outer parts of the dish are "illuminated" with a lower intensity of radiation. Even if the feed provided constant illumination across the angle subtended by the dish, the outer parts of the dish are farther away from the feed antenna than the inner parts, so the intensity would drop off with distance from the center. So the intensity of the beam radiated by a parabolic antenna is maximum at the center of the dish and falls off with distance from the axis, reducing the efficiency.
- Aperture blockage - In front-fed parabolic dishes where the feed antenna is located in front of the dish in the beam path (and in Cassegrain and Gregorian designs as well), the feed structure and its supports block some of the beam. In small dishes such as home satellite dishes, where the size of the feed structure is comparable with the size of the dish, this can seriously reduce the antenna gain. To prevent this problem these types of antennas often use an offset feed, where the feed antenna is located to one side, outside the beam area. The aperture efficiency for these types of antennas can reach 0.7 to 0.8.
- Shape errors - random surface errors in the shape of the reflector reduce efficiency. The loss is approximated by Ruze's Equation.
For theoretical considerations of mutual interference (at frequencies between 2 and c. 30 GHz - typically in the Fixed Satellite Service) where specific antenna performance has not been defined, a reference antenna based on Recommendation ITU-R S.465 is used to calculate the interference, which will include the likely sidelobes for off-axis effects.
Beamwidth
The angular width of the beam radiated by high-gain antennas is measured by the half-power beam width (HPBW), which is the angular separation between the points on the antenna radiation pattern at which the power drops to one-half (-3 dB) its maximum value. For parabolic antennas, the HPBW θ is given by:[4][10]
where k is a factor which varies slightly depending on the shape of the reflector and the feed illumination pattern. For a "typical" parabolic antenna k = 70 when θ is in degrees.[10]
For a typical 2 meter satellite dish operating on C band (4 GHz), like the one shown at right, this formula gives a beamwidth of about 2.6°. For the Arecibo antenna at 2.4 GHz the beamwidth is 0.028°. It can be seen that parabolic antennas can produce very narrow beams, and aiming them can be a problem. Some parabolic dishes are equipped with a boresight so they can be aimed accurately at the other antenna.
It can be seen there is an inverse relation between gain and beam width. By combining the beamwidth equation with the gain equation, the relation is:[10]
See also
- Radio telescope
- Satellite dish
- Simulsat (a quasi parabolic antenna which is spherical in one plane and parabolic in another)
- Corner reflector
References
- ^ Straw, R. Dean, Ed. (2000). The ARRL Antenna Book, 19th Ed.. USA: American Radio Relay League. pp. 19.15. ISBN 0872598179.
- ^ a b c d e f Lehpamer, Harvey (2010). Microwave transmission networks: Planning, Design, and Deployment. USA: McGraw Hill Professional. pp. 268–272. ISBN 0071701222. http://books.google.com/?id=-kiH5WZy88UC&pg=PA263&dq=%22beamwidth%22+%22parabolic+antenna%22#v=onepage&q=%22beamwidth%22%20%22parabolic%20antenna%22&f=false.
- ^ A. David Olver (1994) Microwave Horns and Feeds, p. 61-62
- ^ a b Straw, R. Dean, Ed. (2000). The ARRL Antenna Book, 19th Ed.. USA: American Radio Relay League. pp. 18.14. ISBN 0872598179.
- ^ a b c d e f Olver, A. David (1994). Microwave horns and feeds. USA: IET. pp. 3. ISBN 0780311159. http://books.google.com/books?id=soJiuUwevRIC&pg=PA9&dq=how+horns+work+impedance&hl=en&ei=-V7DTpyxEILJiQKS_InyCw&sa=X&oi=book_result&ct=result&resnum=2&sqi=2&ved=0CDIQ6AEwAQ#v=onepage&q=how%20horns%20work%20impedance&f=false.
- ^ Love, Allan W.. "Large Space Antenna Concepts for ESGP" (PDF). Rockwell International. http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19900009937_1990009937.pdf. Retrieved 2009-07-31.
- ^ Drentea, Cornell (2010). Modern Communications Receiver Design and Technology. USA: Artech House. pp. 369. ISBN 1596933097. http://books.google.com/?id=9juUwbKP-58C&pg=PA369&dq=Arecibo+observatory+%22radio+telescope%22+gain#v=onepage&q=Arecibo%20observatory%20%22radio%20telescope%22%20gain&f=false.
- ^ Anderson, Harry R. (2003). Fixed broadband wireless system design. USA: John Wiley & Sons. pp. 206–207. ISBN 0470844388. http://books.google.com/?id=r-o3SmNsvD8C&pg=PA205&dq=parabolic+antenna+design#v=onepage&q=parabolic%20antenna%20design&f=false.
- ^ Pattan, Bruno (1993). Satellite systems: principles and technologies. USA: Springer. pp. 267. ISBN 0442013574. http://books.google.com/?id=0GJWEro9ea4C&pg=PA267&dq=aperture+efficiency#v=onepage&q=horn%20antenna&f=false.
- ^ a b c Minoli, Daniel (2009). Satellite Systems Engineering in an IPv6 Environment. USA: CRC Press. pp. 78. ISBN 1420078682. http://books.google.com/?id=4yJi1UQDPp8C&pg=PA80&dq=%22beamwidth%22+%22parabolic+antenna%22#v=onepage&q=%22beamwidth%22%20%22parabolic%20antenna%22&f=false.
External links
- WiFi: Parabolic Dish with BiQuad feeder
- Online Satellite Finder Based on Google Maps
- Antenna types: Parabolic Antenna for WiFi
- Online pointing utility using google maps, and each satellite channel list: http://www.dishpointer.com/
- Animation of Propagation from a Parabolic Dish Antenna from Youtube
|
||||||||||||||