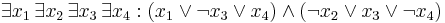PSPACE-complete

In complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time (see complete (complexity)). The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, because a solution to any one such problem could easily be used to solve any other problem in PSPACE. These problems are widely suspected to be outside of the more famous complexity classes P and NP, but that is not known. It is known that they lie outside of the small class NC, since NC is contained in PolyL = DSPACE((log n)^O(1))), which is strictly contained in PSPACE by the space hierarchy theorem.

1 Discussion
2 Examples of PSPACE-complete problems
3 See also
4 References
5 External links

Discussion

The first known PSPACE-complete problem was the word problem for deterministic context-sensitive grammars. In the word problem for context-sensitive grammars, one is given a set of grammatical transformations which can increase, but cannot decrease, the length of a sentence, and wishes to determine if a given sentence could be produced by these transformations. The technical condition of "determinism" (implying roughly that each transformation makes it obvious that it was used) ensures that this process can be solved in polynomial space, and S.-Y. Kuroda's 1964 work "Classes of languages and linear-bounded automata"^[1] showed that any (possibly non-deterministic) program computable in linear space could be converted into the parsing of a context-sensitive grammar, in a way which preserves determinism.

In 1970, Savitch's theorem showed that PSPACE is closed under nondeterminism, implying that even non-deterministic context-sensitive grammars are in PSPACE.

But the archetypal PSPACE-complete problem is generally taken to be the quantified Boolean formula problem (usually abbreviated to QBF or TQBF; the T stands for "true"), a generalization of the first known NP-complete problem, the Boolean satisfiability problem (SAT). The satisfiability problem is the problem of whether there are assignments of truth values to variables that make a Boolean expression true. For example, one instance of SAT would be the question of whether the following is true:

$\exists x_1 \, \exists x_2 \, \exists x_3 \, \exists x_4: (x_1 \or \neg x_3 \or x_4) \and (\neg x_2 \or x_3 \or \neg x_4)$

The quantified Boolean formula problem differs in allowing both universal and existential quantification over the values of the variables:

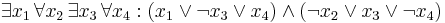$\exists x_1 \, \forall x_2 \, \exists x_3 \, \forall x_4: (x_1 \or \neg x_3 \or x_4) \and (\neg x_2 \or x_3 \or \neg x_4)$ .

The proof that QBF is a PSPACE-complete problem is essentially a restatement of the proof of Savitch's theorem in the language of logic, and is a bit more technical.

Notice that the NP-complete problem resembles a typical puzzle: is there some way to plug in values that solves the problem? The PSPACE-complete problem resembles a game: is there some move I can make, such that for all moves my opponent might make, there will then be some move I can make to win? The question alternates existential and universal quantifiers. Not surprisingly, many puzzles turn out to be NP-complete, and many games turn out to be PSPACE-complete.

Examples of games that are PSPACE-complete (when generalized so that they can be played on an n × n board) are the games hex and Reversi and the solitaire games Rush Hour, Mahjong, Atomix, and Sokoban. Some other generalized games, such as chess, checkers (draughts), and Go are EXPTIME-complete because a game between two perfect players can be very long, so they are unlikely to be in PSPACE. But they will become PSPACE-complete if a polynomial bound on the number of moves is enforced.

Note that the definition of PSPACE-completeness is based on asymptotic complexity: the time it takes to solve a problem of size n, in the limit as n grows without bound. That means a game like checkers (which is played on an 8 × 8 board) could never be PSPACE-complete (in fact, they can be solved in constant time and space using a very large lookup table). That is why all the games were modified by playing them on an n × n board instead; in some cases, such as for Chess, these extensions are somewhat artificial and subjective.

Examples of PSPACE-complete problems

Following are a few PSPACE-complete problems with outlines of the algorithms showing that they are in PSPACE. More examples can be found at list of PSPACE-complete problems.

TQBF

Let TQBF = { <F> : F is a true fully quantified boolean formula }. On input F:
- If F has no quantifier, evaluate and accept iff F is true.
- If F= 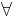$\forall$ pF', recursively evaluate F'[p=1] and F'[p=0], accept iff both accept.
- If F= 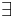$\exist$ qF', recursively evaluate F'[q=1], F'[q=0] and accept iff at least one accept.
Space Usage: The number of levels of recursion is equal to the number of variables of F. The amount of information stored at each level of recursion is constant (values of formula for p=0 and p=1). Therefore the total space used is linear.^[2]

Winning strategies for games

See Game complexity for more games whose completeness for PSPACE or other complexity classes has been determined.

Generalized geography

On input <G,b>:
- If b has no outgoing edge, reject.
- Otherwise, remove b and all its edges, call this new graph G₁.
- Recursively run on inputs <G₁,b_i>, where each b_i are the endpoints of edges from b.
- Reject if all accept; otherwise accept.
Space Usage: The number of levels of recursion is equal to the number of nodes in G. The amount of information stored at each level of recursion is equal to the number of nodes in G. Therefore the total space used is linear.^[2]

Determining if a regular expression generates all strings

Given a regular expression R, determining whether it generates all strings (i.e., L(R) = Σ^*) is PSPACE-complete.

References

Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Section 8.3: PSPACE-completeness, pp. 283–94.
Michael R. Garey and David S. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. Section 7.4: Polynomial Space Completeness, pp. 170–77.

^ "Classes of languages and linear-bounded automata", Information and Control, 7(2): 207–223, June 1964
^ ^a ^b François Pitt. "Lecture Summary for Week 11 work". http://www.cs.utoronto.ca/~fpitt/CSC363/20079/lectures/LN11.txt. Retrieved 2008-02-12.

External links

Important complexity classes (more)

Classes considered feasible	DLOGTIME • AC⁰ • ACC⁰ • TC⁰ • L • SL • RL • NL • NC • SC • P (P-complete) • ZPP • RP • BPP • BQP

Classes suspected to be infeasible	UP • NP (NP-complete · NP-hard · co-NP · co-NP-complete) • AM • PH • PP • #P (#P-complete) • IP • PSPACE (PSPACE-complete)

Classes considered infeasible	EXPTIME • NEXPTIME • EXPSPACE • ELEMENTARY • PR • R • RE • ALL

Class hierarchies	Polynomial hierarchy • Exponential hierarchy • Grzegorczyk hierarchy • Arithmetic hierarchy

Families of complexity classes	DTIME • NTIME • DSPACE • NSPACE • Probabilistically checkable proof • Interactive proof system