PROPT

PROPT
Developer(s) Tomlab Optimization Inc.
Stable release 7.4 / March 24, 2010; 22 months ago (2010-03-24)
Operating system TOMLAB - OS Support
Type Technical computing
License Proprietary
Website PROPT product page

The PROPT[1] MATLAB Optimal Control Software is a new generation platform for solving applied optimal control (with ODE or DAE formulation) and parameters estimation problems.

The platform was developed by MATLAB Programming Contest Winner, Per Rutquist in 2008. The most recent version has support for binary and integer variables as well as an automated scaling module.

Contents

Description

PROPT is a combined modeling, compilation and solver engine, built upon the TomSym modeling class, for generation of highly complex optimal control problems. PROPT uses a pseudospectral Collocation method (with Gauss or Chebyshev points) for solving optimal control problems. This means that the solution takes the form of a Polynomial, and this polynomial satisfies the DAE and the path constraints at the collocation points.

In general PROPT has the following main functions:

Modeling

The PROPT system uses the TomSym symbolic source transformation engine to model optimal control problems. It is possible to define independent variables, dependent functions, scalars and constant parameters:

 toms tf
 toms t
 p = tomPhase('p', t, 0, tf, 30);
 x0 = {tf == 20};
 cbox = {10 <= tf <= 40};
 
 toms z1
 cbox = {cbox; 0 <= z1 <= 500};
 x0 = {x0; z1 == 0};
 
 ki0 = [1e3; 1e7; 10; 1e-3];

States and controls

States and controls only differ in the sense that states need be continuous between phases.

 tomStates x1
 x0 = {icollocate({x1 == 0})};
 
 tomControls u1
 cbox = {-2 <= collocate(u1) <= 1};
 x0 = {x0; collocate(u1 == -0.01)};

Boundary, path, event and integral constraints

A variety of boundary, path, event and integral constraints are shown below:

 cbnd = initial(x1 == 1);       % Starting point for x1
 cbnd = final(x1 == 1);         % End point for x1
 cbnd = final(x2 == 2);         % End point for x2
 pathc = collocate(x3 >= 0.5);  % Path constraint for x3
 intc  = {integrate(x2) == 1};  % Integral constraint for x2
 cbnd = final(x3 >= 0.5);       % Final event constraint for x3
 cbnd = initial(x1 <= 2.0);     % Initial event constraint x1

Single-phase optimal control example

Van der Pol Oscillator [3]

Minimize:

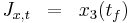
\begin{matrix} J_{x,t} & = & x_3(t_f) \\ \end{matrix}

Subject to:

\begin{cases} \frac{dx_1}{dt} = (1-x_2^2)*x_1-x_2%2Bu \\ \frac{dx_2}{dt} = x_1 \\ \frac{dx_3}{dt} = x_1^2%2Bx_2^2%2Bu^2 \\ x(t_0) = [0 \ 1 \ 0] \\ t_f = 5 \\ -0.3 \le u \le 1.0 \\ \end{cases}

To solve the problem with PROPT the following code can be used (with 60 collocation points):

toms t
p = tomPhase('p', t, 0, 5, 60);
setPhase(p);
 
tomStates x1 x2 x3
tomControls u
 
% Initial guess
x0 = {icollocate({x1 == 0; x2 == 1; x3 == 0})
    collocate(u == -0.01)};
 
% Box constraints
cbox = {-10  <= icollocate(x1) <= 10
    -10  <= icollocate(x2) <= 10
    -10  <= icollocate(x3) <= 10
    -0.3 <= collocate(u)   <= 1};
 
% Boundary constraints
cbnd = initial({x1 == 0; x2 == 1; x3 == 0});
 
% ODEs and path constraints
ceq = collocate({dot(x1) == (1-x2.^2).*x1-x2+u
    dot(x2) == x1; dot(x3) == x1.^2+x2.^2+u.^2});
 
% Objective
objective = final(x3);
 
% Solve the problem
options = struct;
options.name = 'Van Der Pol';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

Multi-phase optimal control example

One-dimensional rocket [4] with free end time and undetermined phase shift

Minimize:

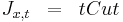
\begin{matrix} J_{x,t} & = & tCut \\ \end{matrix}

Subject to:

\begin{cases} \frac{dx_1}{dt} = x_2 \\ \frac{dx_2}{dt} = a-g \ (0 < t <= tCut) \\ \frac{dx_2}{dt} = -g \ (tCut < t < t_f) \\ x(t_0) = [0 \ 0] \\ g = 1 \\ a = 2 \\ x_1(t_f) = 100 \\ \end{cases}

The problem is solved with PROPT by creating two phases and connecting them:

toms t
toms tCut tp2
p1 = tomPhase('p1', t, 0, tCut, 20);
p2 = tomPhase('p2', t, tCut, tp2, 20);
 
tf = tCut+tp2;
 
x1p1 = tomState(p1,'x1p1');
x2p1 = tomState(p1,'x2p1');
x1p2 = tomState(p2,'x1p2');
x2p2 = tomState(p2,'x2p2');
 
% Initial guess
x0 = {tCut==10
    tf==15
    icollocate(p1,{x1p1 == 50*tCut/10;x2p1 == 0;})
    icollocate(p2,{x1p2 == 50+50*t/100;x2p2 == 0;})};
 
% Box constraints
cbox = {
    1  <= tCut <= tf-0.00001
    tf <= 100
    0  <= icollocate(p1,x1p1)
    0  <= icollocate(p1,x2p1)
    0  <= icollocate(p2,x1p2)
    0  <= icollocate(p2,x2p2)};
 
% Boundary constraints
cbnd = {initial(p1,{x1p1 == 0;x2p1 == 0;})
    final(p2,x1p2 == 100)};
 
% ODEs and path constraints
a = 2; g = 1;
ceq = {collocate(p1,{
    dot(p1,x1p1) == x2p1
    dot(p1,x2p1) == a-g})
    collocate(p2,{
    dot(p2,x1p2) == x2p2
    dot(p2,x2p2) == -g})};
 
% Objective
objective = tCut;
 
% Link phase
link = {final(p1,x1p1) == initial(p2,x1p2)
    final(p1,x2p1) == initial(p2,x2p2)};
 
%% Solve the problem
options = struct;
options.name = 'One Dim Rocket';
constr = {cbox, cbnd, ceq, link};
solution = ezsolve(objective, constr, x0, options);

Parameter estimation example

Parameter estimation problem [5]

Minimize:

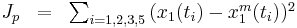
\begin{matrix} J_{p} & = & \sum_{i=1,2,3,5}{(x_1(t_i) - x_1^m(t_i))^2} \\ \end{matrix}

Subject to:

\begin{cases} \frac{dx_1}{dt} = x_2 \\ \frac{dx_2}{dt} = 1-2*x_2-x_1 \\ x_0 = [p_1 \ p_2] \\ t_i = [1 \ 2 \ 3 \ 5] \\ x_1^m(t_i) = [0.264 \ 0.594 \ 0.801 \ 0.959] \\ |p_{1:2}| <= 1.5 \\ \end{cases}

In the code below the problem is solved with a fine grid (10 collocation points). This solution is subsequently fine-tuned using 40 collocation points:

toms t p1 p2
x1meas = [0.264;0.594;0.801;0.959];
tmeas  = [1;2;3;5];
 
% Box constraints
cbox = {-1.5 <= p1 <= 1.5
    -1.5 <= p2 <= 1.5};
 
%% Solve the problem, using a successively larger number collocation points
for n=[10 40]
    p = tomPhase('p', t, 0, 6, n);
    setPhase(p);
    tomStates x1 x2
 
    % Initial guess
    if n == 10
        x0 = {p1 == 0; p2 == 0};
    else
        x0 = {p1 == p1opt; p2 == p2opt
            icollocate({x1 == x1opt; x2 == x2opt})};
    end
 
    % Boundary constraints
    cbnd = initial({x1 == p1; x2 == p2});
 
    % ODEs and path constraints
    x1err = sum((atPoints(tmeas,x1) - x1meas).^2);
    ceq = collocate({dot(x1) == x2; dot(x2) == 1-2*x2-x1});
 
    % Objective
    objective = x1err;
 
    %% Solve the problem
    options = struct;
    options.name   = 'Parameter Estimation';
    options.solver = 'snopt';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
 
    % Optimal x, p for starting point
    x1opt = subs(x1, solution);
    x2opt = subs(x2, solution);
    p1opt = subs(p1, solution);
    p2opt = subs(p2, solution);
end

Optimal control problems supported

References

  1. ^ Rutquist, Per; M. M. Edvall (June 2008). PROPT - Matlab Optimal Control Software. 1260 SE Bishop Blvd Ste E, Pullman, WA 99163, USA: Tomlab Optimization Inc.. http://tomopt.com/docs/TOMLAB_PROPT.pdf. 
  2. ^ Banga, J. R.; Balsa-Canto, E. and Moles, C. G. and Alonso, A. A. (2003). Dynamic optimization of bioprocesses: efficient and robust numerical strategies. Journal of Biotechnology. 
  3. ^ "Van Der Pol Oscillator - Matlab Solution", PROPT Home Page June, 2008.
  4. ^ "One Dimensional Rocket Launch (2 Free Time)", PROPT Home Page June, 2008.
  5. ^ "Matlab Dynamic Parameter Estimation with PROPT", PROPT Home Page June, 2008.
  6. ^ Betts, J. (2007). SOCS Release 6.5.0. THE BOEING COMPANY. 
  7. ^ Liang, J.; Meng, M. and Chen, Y. and Fullmer, R. (2003). Solving Tough Optimal Control Problems by Network Enabled Optimization Server (NEOS). School of Engineering, Utah State University USA, Chinene University of Hong Kong China. 
  8. ^ Carrasco, E. F.; Banga, J. R. (September 1998). A HYBRID METHOD FOR THE OPTIMAL CONTROL OF CHEMICAL PROCESSES. University of Wales, Swansea, UK: UKACC International Conference on CONTROL 98. 
  9. ^ Vassiliadis, V. S.; Banga, J. R. and Balsa-Canto, E. (1999). Second-order sensitivities of general dynamic systems with application to optimal control problems. 54. Chemical Engineering Science. pp. 3851–3860. 
  10. ^ Luus, R. (2002). Iterative dynamic programming. Chapman and Hall/CRC. 
  11. ^ Fabien, B. C. (1998). A Java Application for the Solution of Optimal Control Problems. Stevens Way, Box 352600 Seattle, WA 98195, USA: Mechanical Engineering, University of Washington. 
  12. ^ Jennings, L. S.; Fisher, M. E. (2002). MISER3: Optimal Control Toolbox User Manual, Matlab Beta Version 2.0. Nedlands, WA 6907, Australia: Department of Mathematics, The University of Western Australia. 
  13. ^ Banga, J. R.; Seider, W. D. (1996). Floudas, C. A.; Pardalos, P. M.. eds. Global Optimization of Chemical Processes using Stochastic Algorithms - State of the Art in Global Optimization: Computational Methods and Applications. Dordrecht, The Netherlands: Kluwer Academic Publishers. pp. 563–583. ISBN 0-7923-3838-3 
  14. ^ Dolan, E. D.; More, J. J. (January 2001). Benchmarking Optimization Software with COPS. 9700 South Cass Avenue, Argonne, Illinois 60439: ARGONNE NATIONAL LABORATORY. 

External links