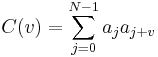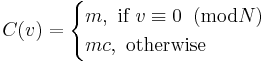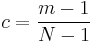Pseudorandom binary sequence
A binary sequence (BS) is a sequence of  bits,
bits,
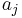 for
for 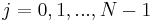 ,
,
i.e.  ones and
ones and 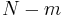 zeros. A BS is pseudo-random (PRBS) if its autocorrelation function:
zeros. A BS is pseudo-random (PRBS) if its autocorrelation function:
has only two values:
where
is called the duty cycle of the PRBS.
A PRBS is random in a sense that the value of an 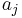 element is independent of the values of any of the other elements, similar to real random sequences.
element is independent of the values of any of the other elements, similar to real random sequences.
It is 'pseudo' because it is deterministic and after  elements it starts to repeat itself, unlike real random sequences, such as sequences generated by radioactive decay or by white noise. The PRBS is more general than the n-sequence, which is a special pseudo-random binary sequence of n bits generated as the output of a linear shift register. An n-sequence always has a 1/2 duty cycle and its number of elements
elements it starts to repeat itself, unlike real random sequences, such as sequences generated by radioactive decay or by white noise. The PRBS is more general than the n-sequence, which is a special pseudo-random binary sequence of n bits generated as the output of a linear shift register. An n-sequence always has a 1/2 duty cycle and its number of elements 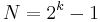 . PRBS's are used in telecommunication, encryption, simulation, correlation technique and time-of-flight spectroscopy.
. PRBS's are used in telecommunication, encryption, simulation, correlation technique and time-of-flight spectroscopy.
Contents |
Practical implementation
Pseudorandom binary sequences can be generated using linear feedback shift registers.[1]
See also
References
- ^ Paul H. Bardell, William H. McAnney, and Jacob Savir, "Built-In Test for VLSI: Pseudorandom Techniques", John Wiley & Sons, New York, 1987.