Ovoid (polar space)

In mathematics, an ovoid O of a (finite) polar space of rank r is a set of points, such that every subspace of rank 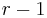$r-1$ intersects O in exactly one point.

1 Cases
2 See also

Cases

Symplectic polar space

An ovoid of 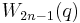$W_{2 n-1}(q)$ (a symplectic polar space of rank n) would contain 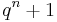$q^n%2B1$ points. However it only has an ovoid if and only 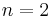$n=2$ and q is even. In that case, when the polar space is embedded into 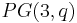$PG(3,q)$ the classical way, it is also an ovoid in the projective geometry sense.

Hermitian polar space

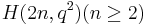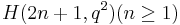Ovoids of $H(2n,q^2)(n\geq 2)$ and $H(2n%2B1,q^2)(n\geq 1)$ would contain 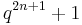$q^{2n%2B1}%2B1$ points.

Hyperbolic quadrics

An ovoid of a hyperbolic quadric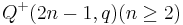 $Q^{%2B}(2n-1,q)(n\geq 2)$ would contain 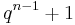$q^{n-1}%2B1$ points.

Parabolic quadrics

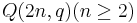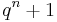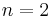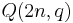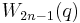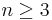An ovoid of a parabolic quadric $Q(2 n,q)(n\geq 2)$ would contain $q^n%2B1$ points. For $n=2$ , it is easy to see to obtain an ovoid by cutting the parabolic quadric with a hyperplane, such that the intersection is an elliptic quadric. The intersection is an ovoid. If q is even, $Q(2n,q)$ is isomorphic (as polar space) with $W_{2 n-1}(q)$ , and thus due to the above, it has no ovoid for $n\geq 3$ .

Elliptic quadrics

An ovoid of an elliptic quadric 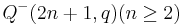$Q^{-}(2n%2B1,q)(n\geq 2)$ would contain 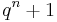$q^{n}%2B1$ points.