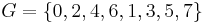Subgroup
| Concepts in group theory | ||||
| category of groups | ||||
| subgroups, normal subgroups | ||||
| group homomorphisms, kernel, image, quotient | ||||
| direct product, direct sum | ||||
| semidirect product, wreath product | ||||
| Types of groups | ||||
|---|---|---|---|---|
| simple, finite, infinite | ||||
| discrete, continuous | ||||
| multiplicative, additive | ||||
| cyclic, abelian, dihedral | ||||
| nilpotent, solvable | ||||
| list of group theory topics | ||||
| glossary of group theory | ||||
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H. This is usually represented notationally by H ≤ G, read as "H is a subgroup of G".
A proper subgroup of a group G is a subgroup H which is a proper subset of G (i.e. H ≠ G). The trivial subgroup of any group is the subgroup {e} consisting of just the identity element. If H is a subgroup of G, then G is sometimes called an overgroup of H.
The same definitions apply more generally when G is an arbitrary semigroup, but this article will only deal with subgroups of groups. The group G is sometimes denoted by the ordered pair (G,*), usually to emphasize the operation * when G carries multiple algebraic or other structures.
This article will write ab for a*b, as is usual.
Contents |
Basic properties of subgroups
- A subset H of the group G is a subgroup of G if and only if it is nonempty and closed under products and inverses. (The closure conditions mean the following: whenever a and b are in H, then ab and a−1 are also in H. These two conditions can be combined into one equivalent condition: whenever a and b are in H, then ab−1 is also in H.) In the case that H is finite, then H is a subgroup if and only if H is closed under products. (In this case, every element a of H generates a finite cyclic subgroup of H, and the inverse of a is then a−1 = an − 1, where n is the order of a.)
- The above condition can be stated in terms of a homomorphism; that is, H is a subgroup of a group G if and only if H is a subset of G and there is an inclusion homomorphism (i.e., i(a) = a for every a) from H to G.
- The identity of a subgroup is the identity of the group: if G is a group with identity eG, and H is a subgroup of G with identity eH, then eH = eG.
- The inverse of an element in a subgroup is the inverse of the element in the group: if H is a subgroup of a group G, and a and b are elements of H such that ab = ba = eH, then ab = ba = eG.
- The intersection of subgroups A and B is again a subgroup.[1] The union of subgroups A and B is a subgroup if and only if either A or B contains the other, since for example 2 and 3 are in the union of 2Z and 3Z but their sum 5 is not. Another example is the union of the x-axis and the y-axis in the plane (with the addition operation); each of these objects is a subgroup but their union is not. This also serves as an example of two subgroups, whose intersection is precisely the identity.
- If S is a subset of G, then there exists a minimum subgroup containing S, which can be found by taking the intersection of all of subgroups containing S; it is denoted by <S> and is said to be the subgroup generated by S. An element of G is in <S> if and only if it is a finite product of elements of S and their inverses.
- Every element a of a group G generates the cyclic subgroup <a>. If <a> is isomorphic to Z/nZ for some positive integer n, then n is the smallest positive integer for which an = e, and n is called the order of a. If <a> is isomorphic to Z, then a is said to have infinite order.
- The subgroups of any given group form a complete lattice under inclusion, called the lattice of subgroups. (While the infimum here is the usual set-theoretic intersection, the supremum of a set of subgroups is the subgroup generated by the set-theoretic union of the subgroups, not the set-theoretic union itself.) If e is the identity of G, then the trivial group {e} is the minimum subgroup of G, while the maximum subgroup is the group G itself.
Cosets and Lagrange's theorem
Given a subgroup H and some a in G, we define the left coset aH = {ah : h in H}. Because a is invertible, the map φ : H → aH given by φ(h) = ah is a bijection. Furthermore, every element of G is contained in precisely one left coset of H; the left cosets are the equivalence classes corresponding to the equivalence relation a1 ~ a2 if and only if a1−1a2 is in H. The number of left cosets of H is called the index of H in G and is denoted by [G : H].
Lagrange's theorem states that for a finite group G and a subgroup H,
where |G| and |H| denote the orders of G and H, respectively. In particular, the order of every subgroup of G (and the order of every element of G) must be a divisor of |G|.
Right cosets are defined analogously: Ha = {ha : h in H}. They are also the equivalence classes for a suitable equivalence relation and their number is equal to [G : H].
If aH = Ha for every a in G, then H is said to be a normal subgroup. Every subgroup of index 2 is normal: the left cosets, and also the right cosets, are simply the subgroup and its complement. More generally, if p is the lowest prime dividing the order of a finite group G, then any subgroup of index p (if such exists) is normal.
Example: Subgroups of Z8
Let G be the cyclic group Z8 whose elements are
and whose group operation is addition modulo eight. Its Cayley table is
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
This group has a pair of nontrivial subgroups: J={0,4} and H={0,2,4,6}, where J is also a subgroup of H. The Cayley table for H is the top-left quadrant of the Cayley table for G. The group G is cyclic, and so are its subgroups. In general, subgroups of cyclic groups are also cyclic.
Example: Subgroups of S4
Every group has as many small subgroups as neutral elements on the main diagonal:
The trivial group and two-element groups Z2. These small subgroups are not counted in the following list.
12 elements
8 elements
6 elements
4 elements
3 elements
See also
Notes
- ^ Jacobson (2009), p. 41
References
- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1.
![[ G�: H ] = { |G| \over |H| }](/2012-wikipedia_en_all_nopic_01_2012/I/398de907f3262d1d9c0d0121eaa87c20.png)