Overring

In mathematics, an overring B of an integral domain A is a subring of the field of fractions K of A that contains A: i.e., 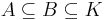$A \subseteq B \subseteq K$ .

A typical example is given by localization: if S is a multiplicatively closed subset of A, then the localization S⁻¹A is an overring of A. In fact, every overring of Z arises in this way.