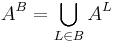Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any complexity class. Even undecidable problems, like the halting problem, can be used.
Contents |
Definition
An oracle machine is a Turing machine connected to an oracle. The oracle, in this context, is thought of as an entity capable of answering some collection of questions, and usually represented as some subset A of the natural numbers. Intuitively then, the oracle machine can perform all of the usual operations of a Turing machine, and can also query the oracle for an answer to a specific question of the form "is x in A?"
The definition given here is one of several possible oracle machine definitions. All these definitions are equivalent, as they agree on which specific functions f can be computed by an oracle machine with oracle A.
An oracle machine, like a Turing machine, includes:
- a work tape: a sequence of cells without beginning or end, each of which may contain a B (for blank) or a 1;
- a read/write head, which rests on a single cell of the work tape and can read the data there, write new data, and move left or right along the tape;
- a control mechanism, which can be in one of a finite number of states, and which will perform different actions (reading data, writing data, moving the control mechanism, and changing states) depending on the current state and the data being read.
In addition to these components, an oracle machine also includes:
- an oracle tape, on which an infinite sequence of B's and 1's is printed, corresponding to the characteristic function of the oracle set A;
- an oracle head, which (like the read/write head) can move left or right along the oracle tape reading data, but which cannot write.
Formal definition
An oracle Turing machine is a 4-tuple 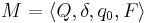 where
where
 is a finite set of states
is a finite set of states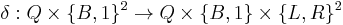 is a partial function called the transition function, where L is left shift, R is right shift.
is a partial function called the transition function, where L is left shift, R is right shift.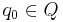 is the initial state
is the initial state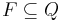 is the set of halting states.
is the set of halting states.
The oracle machine is initialized with the work tape containing some input with finitely many 1's and the rest of the tape blank, the oracle tape containing the characteristic function of the oracle, A, and the Turing machine in state q0 with read/write head reading the first nonblank cell of the work tape, and oracle head reading the cell of the oracle tape which corresponds to 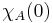 . Thereafter it operates according to
. Thereafter it operates according to  : if the Turing machine is currently in state q, the read/write head is reading a symbol S1, and the oracle head is reading S2, then if
: if the Turing machine is currently in state q, the read/write head is reading a symbol S1, and the oracle head is reading S2, then if 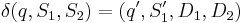 , the machine enters state
, the machine enters state 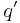 , the read/write head writes the symbol S1' in place of S1, and then the read/write head moves 1 cell in direction D1 and the oracle head moves one cell in direction D2. At this point if
, the read/write head writes the symbol S1' in place of S1, and then the read/write head moves 1 cell in direction D1 and the oracle head moves one cell in direction D2. At this point if 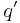 is a halting state, the machine halts, otherwise it repeats this same procedure.
is a halting state, the machine halts, otherwise it repeats this same procedure.
Turing machines can compute functions as follows: if f is a function that takes natural numbers to natural numbers, MA is a Turing machine with oracle A, and whenever MA is initialized with the work tape consisting of n+1 consecutive 1's (and blank elsewhere) MA eventually halts with f(n) 1's on the tape, then MA is said to compute the function f. A similar definition can be made for functions of more than one variable, or partial functions.
If there is an oracle machine M that computes a function f with oracle A, f is said to be A-computable. If f is the characteristic function of a set B, B is also said to be A-computable, and M is said to be a Turing reduction from B to A.
Complexity classes of oracle machines
The complexity class of decision problems solvable by an algorithm in class A with an oracle for a language L is called AL. For example, PSAT is the class of problems solvable in polynomial time by a deterministic Turing machine with an oracle for the Boolean satisfiability problem. The notation AB can be extended to a set of languages B (or a complexity class B), by using the following definition:
When a language L is complete for some class B, then AL=AB provided that machines in A can execute reductions used in the completeness definition of class B. In particular, since SAT is NP-complete with respect to polynomial time reductions, PSAT=PNP. However, if A = DLOGTIME, then ASAT may not equal ANP.
It is obvious that NP ⊆ PNP, but the question of whether NPNP, PNP, NP, and P are equal remains tentative at best. It is believed they are different, and this leads to the definition of the polynomial hierarchy.
Oracle machines are useful for investigating the relationship between complexity classes P and NP, by considering the relationship between PA and NPA for an oracle A. In particular, it has been shown there exist languages A and B such that PA=NPA and PB≠NPB.[1] The fact the P = NP question relativizes both ways is taken as evidence that answering this question is difficult, because a proof technique that relativizes (i.e., unaffected by the addition of an oracle) will not answer the P = NP question. Most proof techniques relativize.
It is interesting to consider the case where an oracle is chosen randomly from among all possible oracles (an infinite set). It has been shown in this case, then with probability 1, PA≠NPA.[2] When a question is true for almost all oracles, it is said to be true for a random oracle. This choice of terminology is justified by the fact random oracles support a statement with probability 0 or 1 only. (This follows from Kolmogorov's zero one law.) This is taken as evidence P≠NP. A statement may be true for a random oracle and false for ordinary Turing machines at the same time; for example for oracles A, IPA≠PSPACEA, while IP = PSPACE.[3]
Oracles and halting problems
It is possible to posit the existence of an oracle which computes a non-computable function, such as the answer to the halting problem or some equivalent. A machine with an oracle of this sort is a hypercomputer.
Interestingly, the halting paradox still applies to such machines; although they determine whether particular Turing machines will halt on particular inputs, they cannot determine, in general, if machines equivalent to themselves will halt. This fact creates a hierarchy of machines, called the arithmetical hierarchy, each with a more powerful halting oracle and an even harder halting problem.
Applications to cryptography
In cryptography, oracles are used to make arguments for the security of cryptographic protocols where a hash function is used. A security reduction for the protocol is given in the case where, instead of a hash function, a random oracle answers each query but consistently; the oracle assumes to be available to all parties including the attacker, as the hash function is. Such a proof shows unless the attacker solves the hard problem at the heart of the security reduction, they must make use of some interesting property of the hash function to break the protocol; they cannot treat the hash function as a black box (i.e., as a random oracle).
See also
References
- ^ T. P. Baker, J. Gill, R. Solovay. Relativizations of the P =? NP Question. SIAM Journal on Computing, 4(4): 431-442 (1975)
- ^ C. H. Bennett, J. Gill. Relative to a Random Oracle A, PA != NPA != co-NPA with Probability 1. SIAM Journal on Computing, 10(1): 96-113 (1981)
- ^ Richard Chang, Benny Chor, Oded Goldreich, Juris Hartmanis, Johan Hastad, Desh Ranjan, Pankaj Rohatgi. The Random Oracle Hypothesis is False. Journal of Computer and System Sciences, volume 49, issue 1, pp.24–39. August 1994. ISSN 0022-0000. http://citeseer.ist.psu.edu/282397.html
Further reading
- Alan Turing, Systems of logic based on ordinals, Proc. London math. soc., 45, 1939
- C. Papadimitriou. Computational Complexity. Addison-Wesley, 1994. Section 14.3: Oracles, pp. 339–343.
- Michael Sipser. Introduction to the Theory of Computation. PWS Publishing, 1997. ISBN 0-534-94728-X. Section 9.2: Relativization, pp.318–321.
- Martin Davis, editor: The Undecidable, Basic Papers on Undecidable Propositions, Unsolvable Problems And Computable Functions, Raven Press, New York, 1965. Turing's paper is in this volume. Papers include those by Godel, Church, Rosser, Kleene, and Post.