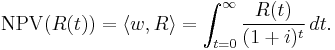One-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.
In differential geometry, a one-form on a differentiable manifold is a smooth section of the cotangent bundle. Equivalently, a one-form on a manifold M is a smooth mapping of the total space of the tangent bundle of M to R whose restriction to each fibre is a linear functional on the tangent space. Symbolically,
where αx is linear.
Often one-forms are described locally, particularly in local coordinates. In a local coordinate system, a one-form is a linear combination of the differentials of the coordinates:
where the fi are smooth functions. Note the use of upper numerical indices, not to be confused with powers. From this perspective, a one-form has a covariant transformation law on passing from one coordinate system to another. Thus a one-form is an order 1 covariant tensor field.
Contents |
Examples
Many real-world concepts can be described as one-forms:
- Indexing into a vector: The second element of a three-vector is given by the one-form [0, 1, 0]. That is, the second element of [x ,y ,z] is
-
- [0, 1, 0] · [x, y, z] = y.
- Mean: The mean element of an n-vector is given by the one-form [1/n, 1/n, ..., 1/n]. That is,
- Sampling: Sampling with a kernel can be considered a one-form, where the one-form is the kernel shifted to the appropriate location.
- Net present value of a net cash flow, R(t), is given by the one-form w(t) := (1 + i)−t where i is the discount rate. That is,
Differential of a function
-
Main article: Differential of a function
Let 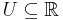 be open (e.g., an interval
be open (e.g., an interval 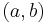 ), and consider a differentiable function
), and consider a differentiable function 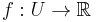 , with derivative f'. The differential df of f, at a point
, with derivative f'. The differential df of f, at a point 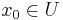 , is defined as a certain linear map of the variable dx. Specifically,
, is defined as a certain linear map of the variable dx. Specifically, 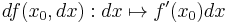 . (The meaning of the symbol dx is thus revealed: it is simply an argument, or independent variable, of the function df.) Hence the map
. (The meaning of the symbol dx is thus revealed: it is simply an argument, or independent variable, of the function df.) Hence the map 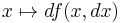 sends each point x to a linear functional df(x,dx). This is the simplest example of a differential (one-)form.
sends each point x to a linear functional df(x,dx). This is the simplest example of a differential (one-)form.
In terms of the de Rham complex, one has an assignment from zero-forms (scalar functions) to one-forms i.e., 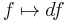 .
.
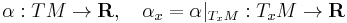
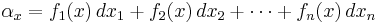
![\operatorname{mean}(v) = [1/n, 1/n,\dots,1/n]\cdot v.](/2012-wikipedia_en_all_nopic_01_2012/I/edfd717c7e1a9aa1a4f51885c677ccbb.png)