Olog
Olog is a term that was coined from ontology (onto-, from the Greek ὤν, ὄντος "being; that which is", present participle of the verb εἰμί "be", and -λογία, -logia: science, study, theory) logs, a concept introduced in 2010 by David Spivak,[1] a postdoctoral associate in the Department of Mathematics, MIT. Ologs provide an abstract means for categorizing the general properties of a system – be it a material, mathematical concept or phenomenon – and showing inherent relationships between function and structure.
The concept was experimentally documented by David Spivak and coauthors Associate Professor Markus J. Buehler of the Department of Civil and Environmental Engineering (CEE) and CEE graduate student Tristan Giesa in a paper that was published in the December 2011 issue of BioNanoScience[2] in which the researchers establish a scientific analogy between spider silk and musical composition. The methodology represents a new approach to the comparison of research findings in disparate scientific fields. Such analogies could help engineers develop materials that make use of the repeating patterns of simple building blocks found in many biological materials that, like spider silk, are lightweight yet extremely failure-resistant. The work also suggests that engineers may be able to gain new insights into biological systems through the study of the structure-function relationships found in music and other art forms.[3][4]
Contents |
Underlying mathematics
Ologs are essentially categories, or more precisely sketches, except with a linguistic naming system on boxes and arrows that make an intention clear. Given an olog  , a functor (or sketch map)
, a functor (or sketch map) 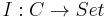 is called an instance of the olog, in keeping with the terminology used for databases. The reason is that an olog can serve as a relational database schema in a straightforward way.[5] If an olog represents a world-view or conceptual understanding in some domain, an instance of that olog keeps track of experience or examples for this understanding.
is called an instance of the olog, in keeping with the terminology used for databases. The reason is that an olog can serve as a relational database schema in a straightforward way.[5] If an olog represents a world-view or conceptual understanding in some domain, an instance of that olog keeps track of experience or examples for this understanding.
A functor (or span) 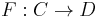 connecting different ologs serves as a language translation system. Once in place, examples (instances) can be transported in various ways using pushforward and pullback functors (often denoted
connecting different ologs serves as a language translation system. Once in place, examples (instances) can be transported in various ways using pushforward and pullback functors (often denoted 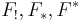 ).
).
See also
References
- ^ http://arxiv.org/abs/1102.1889v1
- ^ BioNanoScience Volume 1, Number 4, 153–161, DOI: 10.1007/s12668-011-0022-5 Reoccurring Patterns in Hierarchical Protein Materials and Music: The Power of Analogies Tristan Giesa, David I. Spivak and Markus J. Buehler
- ^ http://www.sciencedaily.com/releases/2011/12/111208092602.htm
- ^ http://cee.mit.edu/news/releases/2011/spider-silk-music-olog
- ^ http://arxiv.org/abs/1009.1166
External links
- MIT site [1]
- Sciencedaily [2]
- BioNanoScience: Reoccurring Patterns in Hierarchical Protein Materials and Music: The Power of Analogies
Tristan Giesa, David I. Spivak and Markus J. Buehler [3]