Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold 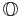 . There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H. The octonions are the largest such algebra, with eight dimensions, double the number of the quaternions from which they are an extension. They are noncommutative and nonassociative, but satisfy a weaker form of associativity, power associativity.
. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H. The octonions are the largest such algebra, with eight dimensions, double the number of the quaternions from which they are an extension. They are noncommutative and nonassociative, but satisfy a weaker form of associativity, power associativity.
|
Octonions are not as well known as the quaternions and complex numbers, which are much more widely studied and used. Despite this they have some interesting properties and are related to a number of exceptional structures in mathematics, among them the exceptional Lie groups. Additionally, octonions have applications in fields such as string theory, special relativity, and quantum logic.
The octonions were discovered in 1843 by John T. Graves, inspired by his friend William Hamilton's discovery of quaternions. Graves called his discovery octaves. They were discovered independently by Arthur Cayley[1] and are sometimes referred to as Cayley numbers or the Cayley algebra.
Definition
The octonions can be thought of as octets (or 8-tuples) of real numbers. Every octonion is a real linear combination of the unit octonions:
where e0 is the scalar or real element; it may be identified with the real number 1. That is, every octonion x can be written in the form
with real coefficients {xi}.
Addition and subtraction of octonions is done by adding and subtracting corresponding terms and hence their coefficients, like quaternions. Multiplication is more complex. Multiplication is distributive over addition, so the product of two octonions can be calculated by summing the product of all the terms, again like quaternions. The product of each term can be given by multiplication of the coefficients and a multiplication table of the unit octonions, like this one:[2]
| × | e0 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
|---|---|---|---|---|---|---|---|---|
| e0 | e0 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| e1 | e1 | −e0 | e3 | −e2 | e5 | −e4 | −e7 | e6 |
| e2 | e2 | −e3 | −e0 | e1 | e6 | e7 | −e4 | −e5 |
| e3 | e3 | e2 | −e1 | −e0 | e7 | −e6 | e5 | −e4 |
| e4 | e4 | −e5 | −e6 | −e7 | −e0 | e1 | e2 | e3 |
| e5 | e5 | e4 | −e7 | e6 | −e1 | −e0 | −e3 | e2 |
| e6 | e6 | e7 | e4 | −e5 | −e2 | e3 | −e0 | −e1 |
| e7 | e7 | −e6 | e5 | e4 | −e3 | −e2 | e1 | −e0 |
Most off-diagonal elements of the table are antisymmetric, making it almost a skew-symmetric matrix except for the elements on the main diagonal, the row and the column for which e0 is an operand.
The table can be summarized by the relations:[3]
where 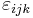 is a completely antisymmetric tensor with value +1 when ijk = 123, 145, 176, 246, 257, 347, 365, and:
is a completely antisymmetric tensor with value +1 when ijk = 123, 145, 176, 246, 257, 347, 365, and:
with e0 the scalar element, and i, j, k = 1 ... 7.
The above definition though is not unique, but is only one of a 480 possible definitions for octonion multiplication. The others can be obtained by permuting the non-scalar elements, so can be considered to have different bases. Alternately they can be obtained by fixing the product rule for a few terms, and deducing the rest from the other properties of the octonions. The 480 different algebras are isomorphic, so are in practice identical, and there is rarely a need to consider which particular multiplication rule is used.[4][5]
Cayley–Dickson construction
A more systematic way of defining the octonions is via the Cayley–Dickson construction. Just as quaternions can be defined as pairs of complex numbers, the octonions can be defined as pairs of quaternions. Addition is defined pairwise. The product of two pairs of quaternions (a, b) and (c, d) is defined by
where 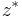 denotes the conjugate of the quaternion z. This definition is equivalent to the one given above when the eight unit octonions are identified with the pairs
denotes the conjugate of the quaternion z. This definition is equivalent to the one given above when the eight unit octonions are identified with the pairs
- (1,0), (i,0), (j,0), (k,0), (0,1), (0,i), (0,j), (0,k)
Fano plane mnemonic
A convenient mnemonic for remembering the products of unit octonions is given by the diagram at the right, which represents the multiplication table of Cayley and Graves.[2][6] This diagram with seven points and seven lines (the circle through 1, 2, and 3 is considered a line) is called the Fano plane. The lines are oriented. The seven points correspond to the seven standard basis elements of Im(O) (see definition below). Each pair of distinct points lies on a unique line and each line runs through exactly three points.
Let (a, b, c) be an ordered triple of points lying on a given line with the order specified by the direction of the arrow. Then multiplication is given by
- ab = c and ba = −c
together with cyclic permutations. These rules together with
- 1 is the multiplicative identity,
- ei2 = −1 for each point in the diagram
completely defines the multiplicative structure of the octonions. Each of the seven lines generates a subalgebra of O isomorphic to the quaternions H.
Conjugate, norm, and inverse
The conjugate of an octonion
is given by
Conjugation is an involution of O and satisfies (xy)*=y* x* (note the change in order).
The real part of x is given by
and the imaginary part by
The set of all purely imaginary octonions span a 7 dimension subspace of O, denoted Im(O).
Conjugation of octonions satisfies the equation
The product of an octonion with its conjugate, x* x = x x*, is always a nonnegative real number:
Using this the norm of an octonion can be defined, as
This norm agrees with the standard Euclidean norm on R8.
The existence of a norm on O implies the existence of inverses for every nonzero element of O. The inverse of x ≠ 0 is given by
It satisfies x x−1 = x−1 x = 1.
Properties
Octonionic multiplication is neither commutative:
nor associative:
The octonions do satisfy a weaker form of associativity: they are alternative. This means that the subalgebra generated by any two elements is associative. Actually, one can show that the subalgebra generated by any two elements of O is isomorphic to R, C, or H, all of which are associative. Because of their non-associativity, octonions don't have matrix representations, unlike quaternions.
The octonions do retain one important property shared by R, C, and H: the norm on O satisfies
This implies that the octonions form a nonassociative normed division algebra. The higher-dimensional algebras defined by the Cayley–Dickson construction (e.g. the sedenions) all fail to satisfy this property. They all have zero divisors.
Wider number systems exist which have a multiplicative modulus (e.g. 16 dimensional conic sedenions). Their modulus is defined differently from their norm, and they also contain zero divisors.
It turns out that the only normed division algebras over the reals are R, C, H, and O. These four algebras also form the only alternative, finite-dimensional division algebras over the reals (up to isomorphism).
Not being associative, the nonzero elements of O do not form a group. They do, however, form a loop, indeed a Moufang loop.
Commutator and cross product
The commutator of two octonions x and y is given by
This is antisymmetric and imaginary. If it is considered only as a product on the imaginary subspace Im(O) it defines a product on that space, the seven-dimensional cross product, given by
Like the cross product in three dimensions this is a vector orthogonal to x and y with magnitude
But like the octonion product it is not uniquely defined. Instead there are are many different cross products, each one dependent on the choice of octonion product.[7]
Automorphisms
An automorphism, A, of the octonions is an invertible linear transformation of O which satisfies
The set of all automorphisms of O forms a group called G2. The group G2 is a simply connected, compact, real Lie group of dimension 14. This group is the smallest of the exceptional Lie groups and is isomorphic to the subgroup of SO(7) that preserves any chosen particular vector in its 8-dimensional real spinor representation.
See also: PSL(2,7) - the automorphism group of the Fano plane.
In-line sources and notes
- ^ Arthur Cayley (1845)
- ^ a b This table is due to Arthur Cayley (1845) and John T. Graves (1843). See G Gentili, C Stoppato, DC Struppa and F Vlacci (2009), "Recent developments for regular functions of a hypercomplex variable", in Irene Sabadini, M Shapiro, F Sommen, Hypercomplex analysis (Conference on quaternionic and Clifford analysis; proceedings ed.), Birkaüser, p. 168, ISBN 9783764398927, http://books.google.com/?id=H-5v6pPpyb4C&pg=PA168
- ^ Lev Vasilʹevitch Sabinin, Larissa Sbitneva, I. P. Shestakov (2006), "§17.2 Octonion algebra and its regular bimodule representation", Non-associative algebra and its applications, CRC Press, p. 235, ISBN 0824726693, http://books.google.com/?id=_PEWt18egGgC&pg=PA235
- ^ Rafał Abłamowicz, Pertti Lounesto, Josep M. Parra (1996), "§ Four ocotonionic basis numberings", Clifford algebras with numeric and symbolic computations, Birkhäuser, p. 202, ISBN 0817639071, http://books.google.com/?id=OpbY_abijtwC&pg=PA202
- ^ Jörg Schray, Corinne A. Manogue (1996), "Octonionic representations of Clifford algebras and triality", Foundations of physics (Springer) 26 (Number 1/January): 17–70, doi:10.1007/BF02058887, http://www.springerlink.com/content/w1884mlmj88u5205/. Available as ArXive preprint Figure 1 is located here.
- ^ Tevian Dray & Corrine A Manogue (2004), "Chapter 29: Using octonions to describe fundamental particles", in Pertti Lounesto, Rafał Abłamowicz, Clifford algebras: applications to mathematics, physics, and engineering, Birkhäuser, p. 452, ISBN 0817635254, http://books.google.com/?id=b6mbSCv_MHMC&pg=PA452 Figure 29.1: Representation of multiplication table on projective plane.
- ^ Baez (2002) p 37-38
See also
References
- Baez, John (2002), "The Octonions", Bull. Amer. Math. Soc. 39 (02): 145–205, doi:10.1090/S0273-0979-01-00934-X, http://www.ams.org/bull/2002-39-02/S0273-0979-01-00934-X/home.html. Online HTML versions at Baez's site or see lanl.arXiv.org copy
- Cayley, Arthur (1845), "On Jacobi's elliptic functions, in reply to the Rev..; and on quaternions", Philos. Mag. 26: 208–211. Appendix reprinted in The Collected Mathematical Papers, Johnson Reprint Co., New York, 1963, p. 127.
- Conway, John Horton; Smith, Derek A. (2003), On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd., ISBN 1-56881-134-9. (Review).
External links
|
|||||||||||
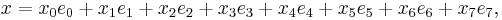
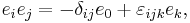
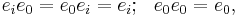
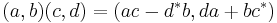
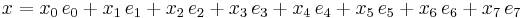
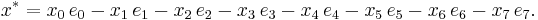
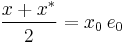
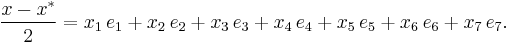
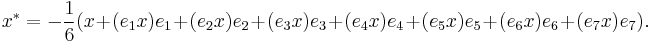
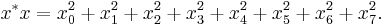
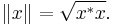
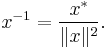
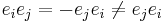
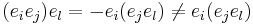
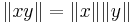
![[x, y] = xy - yx.\,](/2012-wikipedia_en_all_nopic_01_2012/I/8b644d8995387703cf750813b7ccb3b0.png)
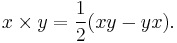
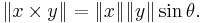
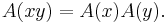
 )
) )
)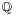 )
)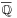 )
)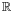 )
)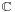 )
)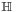 )
)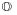 )
)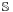 )
)