Nullcline
Nullclines, sometimes called zero-growth isoclines, are encountered in a system of ordinary differential equations
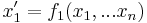
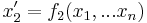
- .
- .
- .
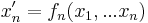
where the 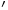 here represents a derivative with respect to another parameter, such as time
here represents a derivative with respect to another parameter, such as time  . Nullclines are the geometric shape for which
. Nullclines are the geometric shape for which 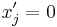 for any
for any  . The fixed points of the system are located where all of the nullclines intersect. In a two-dimensional linear system, the nullclines can be represented by two lines on a two-dimensional plot.
. The fixed points of the system are located where all of the nullclines intersect. In a two-dimensional linear system, the nullclines can be represented by two lines on a two-dimensional plot.