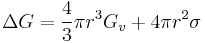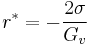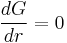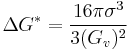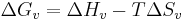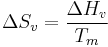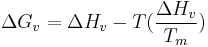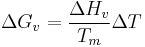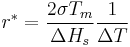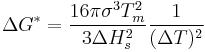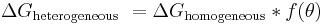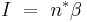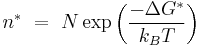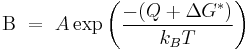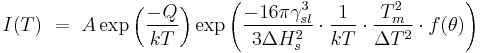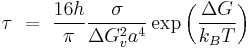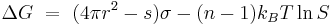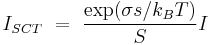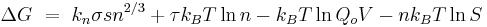Nucleation

Not to be confused with Microtubule nucleation.

Nucleation is the extremely localized budding of a distinct thermodynamic phase. Some examples of phases that may form by way of nucleation in liquids are gaseous bubbles, crystals or glassy regions. Creation of liquid droplets in saturated vapor is also characterized by nucleation (see Cloud condensation nuclei). Nucleation of crystalline, amorphous and even vacancy clusters solid materials is also important, for example to the semiconductor industry. Most nucleation processes are physical, rather than chemical, but a few exceptions do exist (e.g. electrochemical nucleation). A good example would be the famous Diet Coke and Mentos eruption. Nucleation normally occurs at nucleation sites on surfaces contacting the liquid or vapor. Suspended particles or minute bubbles also provide nucleation sites. This is called heterogeneous nucleation. Nucleation without preferential nucleation sites is homogeneous nucleation. Homogeneous nucleation occurs spontaneously and randomly, but it requires superheating or supercooling of the medium. Nucleation is involved in such processes as cloud seeding and in instruments such as the bubble chamber and the cloud chamber.

1 Examples of nucleation
2 Mechanics of nucleation
3 Modern Theory
- 3.1 Classical nucleation
- 3.2 Modifications
4 Modern technology
5 Experimental
6 Footnotes

Examples of nucleation

Presence of cloud condensation nuclei is important in meteorology because they are often in short supply in the upper atmosphere (see cloud seeding).
All natural and artificial crystallization process (of formation of solid crystals from a homogeneous solution) starts with a nucleation event.
Bubbles of carbon dioxide nucleate shortly after the pressure is released from a container of carbonated liquid. Nucleation often occurs more easily at a pre-existing interface (heterogeneous nucleation), as happens on boiling chips and string used to make rock candy. So-called Diet Coke and Mentos eruptions are a dramatic example.
Nucleation in boiling can occur in the bulk liquid if the pressure is reduced so that the liquid becomes superheated with respect to the pressure-dependent boiling point. More often nucleation occurs on the heating surface, at nucleation sites. Typically, nucleation sites are tiny crevices where free gas-liquid surface is maintained or spots on the heating surface with lower wetting properties. Substantial superheating of a liquid can be achieved after the liquid is de-gassed and if the heating surfaces are clean, smooth and made of materials well wetted by the liquid.
Nucleation is relevant in the process of crystallization of nanometer sized materials,^[1] and plays an important role in atmospheric processes.
Nucleation is a key concept in polymer,^[2] alloy and ceramic systems.
In chemistry and biophysics, nucleation can also refer to the phaseless formation of multimers which are intermediates in polymerization processes. This sort of process is believed to be the best model for processes such as crystallization and amyloidogenesis.
In molecular biology, nucleation is the term used to describe the critical stage in the assembly of a polymeric structure, such as a microfilament, at which a small cluster of monomers aggregates in the correct arrangement to initiate rapid polymerization. For instance, two actin molecules bind weakly, but addition of a third stabilizes the complex. This trimer then adds additional molecules and forms a nucleation site. The nucleation site serves the slow, or lag phase of the polymerization process.
Some champagne stirrers operate by providing many nucleation sites via high surface area and sharp corners, speeding the release of bubbles and removing carbonation from the wine.
Sodium acetate heating pads use cavitation voids caused by the deflection of a metal disk as nucleation centres for exothermic crystallization.

Mechanics of nucleation

Homogeneous nucleation

Nucleation generally occurs with much more difficulty in the interior of a uniform substance, by a process called homogeneous nucleation. The creation of a nucleus implies the formation of an interface at the boundaries of a new phase.

Liquids cooled below the maximum heterogeneous nucleation temperature (melting temperature), but which are above the homogeneous nucleation temperature (pure substance freezing temperature) are said to be supercooled. This is useful for making amorphous solids and other metastable structures, but can delay the progress of industrial chemical processes or produce undesirable effects in the context of casting. Supercooling brings about supersaturation, the driving force for nucleation. Supersaturation occurs when the pressure in the newly formed solid is less than the liquid pressure, and brings about a change in free energy per unit volume, 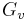$G_v$ , between the liquid and newly created solid phase. This change in free energy is balanced by the energy gain of creating a new volume, and the energy cost due to creation of a new interface. When the overall change in free energy, 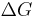$\Delta G$ is negative, nucleation is favored.

Some energy is consumed to form an interface, based on the surface energy of each phase. If a hypothetical nucleus is too small (known as an unstable nucleus or "embryo"), the energy that would be released by forming its volume is not enough to create its surface, and nucleation does not proceed. The critical nucleus size can be denoted by its radius, and it is when r=r* (or r critical) that the nucleation proceeds.

For example in the classic case^[3] of a spherical cluster that liberates -G_v Joules per cubic centimeter during formation (here G_v is a negative quantity), but which must pay the positive cost of σ Joules per square centimeter of surface interfacing with the surrounding, the free energy needed to form a spherical cluster of radius r is,

$\Delta G = \frac{4}{3} \pi r^3 G_v %2B 4 \pi r^2 \sigma$

Where the first term shows the energy gain of creating a new volume and the second term shows the energy loss due to surface tension ( $\sigma$ ) of the new interface.

It costs free energy to add molecules to this cluster (because 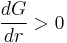$\frac{dG}{dr} > 0$ ) until the radius reaches,

$r^* = -\frac{2 \sigma}{G_v}$

where,

$\frac{dG}{dr} = 0$

Addition of new molecules to clusters larger than this critical radius releases, rather than costs, available work. In other words at that point growth of the cluster is no longer limited by nucleation, but perhaps by diffusion^[4] (i.e. the supply of molecules) or by reaction kinetics instead.

The free energy needed to form this critical radius can be found by

$\Delta G^* = \frac{16 \pi \sigma ^3}{3(G_v)^2}$

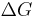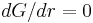
which occurs at the maximum $\Delta G$ where $dG/dr=0$
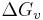The term $\Delta G_v$ can be related to the equilibrium temperature, enthalpy of fusion ( 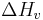$\Delta H_v$ ), and the degree of undercooling ( 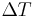$\Delta T$ ) as follows,

$\Delta G_v=\Delta H_v - T \Delta S_v$

By evaluating this equation at the equilibrium point (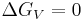 $\Delta G_V = 0$ ) at the melting temperature 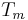$T_m$ we achieve,

$\Delta S_v=\frac{\Delta H_v}{T_m}$

Substitution of 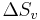$\Delta S_v$ into the first equation leads to,

$\Delta G_v=\Delta H_v - T(\frac{\Delta H_v}{T_m})$

Which by using common denominators and the definition of 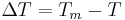$\Delta T = T_m-T$ provides,

$\Delta G_v=\frac{\Delta H_v}{T_m}\Delta T$

As the phase transformation becomes more and more favorable, the formation of a given volume of nucleus frees enough energy to form an increasingly large surface, allowing progressively smaller nuclei to become viable. Eventually, thermal activation will provide enough energy to form stable nuclei. These can then grow until thermodynamic equilibrium is restored.

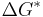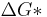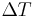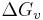A greater degree of supercooling favors phase transformation, and we can relate $\Delta G^*$ to supercooling and find r* and $\Delta G*$ as a function of $\Delta T$ by the substitution of $\Delta G_v$ ,

$r^* = \frac{2 \sigma T_m}{\Delta H_s} \frac{1}{\Delta T}$

and

$\Delta G^* = \frac{16 \pi \sigma ^3 T_m^2}{3\Delta H_s^2} \frac{1}{(\Delta T)^2}$

The greater the supercooling, the smaller the critical radius and the less energy needed to form it.

The spontaneous nucleation rate in, say, water changes very rapidly with temperature, so the spontaneous nucleation temperature can be quite well defined. 'Film boiling' on very hot surfaces and the Leidenfrost effect are both believed to be stabilized by spontaneous nucleation phenomena.

Heterogeneous nucleation

Heterogeneous nucleation occurs much more often than homogeneous nucleation. It forms at preferential sites such as phase boundaries or impurities like dust and requires less energy than homogeneous nucleation. At such preferential sites, the effective surface energy is lower, thus diminishing the free energy barrier and facilitating nucleation. Surfaces promote nucleation because of wetting – contact angles greater than zero between phases encourage particles to nucleate. The free energy needed for heterogeneous nucleation is equal to the product of homogeneous nucleation and a function of the contact angle :

$\Delta G_\mathrm{heterogeneous}\ = \Delta G_\mathrm{homogeneous}*f( \theta)$

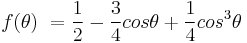
where $f( \theta)\ = \frac{1}{2} - \frac{3}{4}cos\theta %2B \frac{1}{4}cos^3 \theta$

The barrier energy needed for heterogeneous nucleation is reduced, and less supercooling is needed. The wetting angle determines the ease of nucleation by reducing the energy needed. The critical radius remains unchanged: however, the volume can be significantly less for heterogeneous nucleation due to the wetting angle affecting the shape of the cluster.

In the case of heterogeneous nucleation, some energy is released by the partial destruction of the previous interface. For example, if a carbon dioxide bubble forms between water and the inside surface of a bottle, the energy inherent in the water-bottle interface is released wherever a layer of gas intervenes, and this energy goes toward the formation of bubble-water and bubble-bottle interfaces. The same effect can cause precipitate particles to form at the grain boundaries of a solid. This can interfere with precipitation strengthening, which relies on homogeneous nucleation to produce a uniform distribution of precipitate particles.

Rate of nucleation

The nucleation rate, I, depends on the average number of critical clusters, n* and the diffusion of molecules to the cluster, $\beta$ .

$I\ =\ n^* \beta$

where the average population of critical nuclei is

$n^*\ =\ N \exp \left( \frac{-\Delta G^*}{k_BT} \right)$

where:

ΔG* is critical free energy needed corresponding to that of the critical radius.
N is the number of potential nucleation sites per unit volume
k_B is the Boltzmann constant

The number of clusters of a certain size formed is a function of the total number of atoms in the system, the free energy to create a cluster (of that size), and the temperature. The number of clusters increases with increasing temperature.

Plugging in for 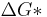$\Delta G*$ , we get

The rate of addition of one extra atom to the critical nucleus as estimated by the Volmer-Weber theory is

$\Beta\ =\ A \exp \left( \frac{-(Q %2B \Delta G^*)}{k_BT} \right)$

where A is a term that incorporates the shape factor of the atoms and the area to which atoms can join, and the vibrational frequency of the particles. And Q is the activation energy for atomic migration.

This term gives us the diffusion of the atoms to the site of nucleation. However, a problem with the Volmer Weber theory is that it ignores formation of particles of r>r* and assumes that size distribution is maintained (fluctuations are occurring fast)

The rate of nucleation can be expressed as:

$I(T)\ =\ A \exp \left( \frac{-Q}{kT} \right) \exp \left( \frac{-16 \pi \gamma_{sl}^3}{3 \Delta H_s^2} \cdot \frac{1}{kT} \cdot \frac{T_m^2}{\Delta T^2} \cdot f(\theta) \right)$

Where:

γ is the surface tension.
ΔH_s is the enthalpy per unit volume.
Tm is the melting temperature.
Θ is the wetting angle.

At very low temperatures, rate of diffusion is low. As temperature increases, the rate of diffusion increases; molecules are able to get to the site of nucleation at a fast enough rate to promote growth of the nucleus. At temperatures significantly below melting temperature, fluctuation of molecules is very low; the molecules are in a low energy state and do not have enough energy to move around and nucleate. Nucleation rate is dominated by diffusion. However, as temperature increases, molecular fluctuations increase and molecules tend to escape from the nucleus, causing a decreased rate of nucleation.

The time required for steady state nucleation is known as the time-lag $\tau$ and can be found by^[5]

$\tau\ =\ \frac{16h}{\pi} \frac{\sigma}{\Delta G_v^2a^4} \exp\left( \frac{\Delta G}{k_BT} \right)$

Where:

a is the average particle size.

The spinodal region

Phase transition processes can also be explained in terms of spinodal decomposition where phase separation is delayed until the system enters the unstable region where a small perturbation in composition leads to a decrease in energy and thus spontaneous growth of the perturbation.^[6] This region of a phase diagram is known as the spinodal region and the phase separation process is known as spinodal decomposition and may be governed by the Cahn–Hilliard equation.

Modern Theory

Classical nucleation

Due to the many unjustified assumptions made by the classical nucleation theory (CNT), it has limited applicability to the solution of practical problems when compared with experimental data. The limitations arise mainly because the CNT assumes that macroscopic properties of molecules can be applied to microscopic activities. This can be a major drawback when dealing with characteristics such as density, surface tension, and saturated vapour pressure of clusters consisting of only several tens of molecules. The classical nucleation theory also does not take into consideration the interaction of particles around the nuclei, which leads to thermodynamics.

Modifications

In the last five decades, due to the ever- increasing accuracy of experimental results, many scientists and engineers have worked to improve and develop more accurate nucleation models. One of the versions of the classical theory which has gained acceptance is the self-consistent theory (SCT) of nucleation.^[7] According to this theory,

$\Delta G\ =\ (4 \pi r^2 - s) \sigma - (n - 1)k_BT \ln S$

Where:

ΔG is critical free energy needed.
k_B is the Boltzmann constant
S=p_v/p_o is the supersaturation
s is the surface area of a monomer

Under this theory, the nucleation rate becomes

$I_{SCT}\ =\ \frac{\exp(\sigma s/ k_BT)}{S}I$

Where I is the rate calculated from the classical nucleation theory. The exponential coefficient in the equation takes into account the surface energy of the monomer.

Another popular modern nucleation theory is the Dillmann-Meier theory where the change in free energy is expressed as

$\Delta G\ =\ k_n \sigma sn^{2/3} %2B \tau k_B T \ln n - k_BT\ln Q_oV - nk_BT \ln S$

Where:

τ,k_n and q_o are adjustable coefficients of the model
V is the volume of the system

The coefficient k_n reflects the difference between the surface energies of the cluster and the macroscopic liquid droplet and is represented in the first term of the equation. The second and third term takes into account the translational, vibrational and rotational degrees of freedom to the free energy of the droplet. Lastly the fourth term takes into account relaxation of the metastable state. Many scientists believe this equation takes into account all significant contributions to the energy of cluster formation.^[8]

Although these modern modifications to the classical nucleation theory improve the applicability of the model, further exploration is still going on to either improve or develop a better model that can be applied to a wider range of conditions.

Modern technology

Nucleation is a topic of wide interest in many scientific studies and technological processes. It is used heavily in the chemical industry for cases such as in the preparation of metallic ultradispersed powders that can serve as catalysts. For example, platinum deposited onto TiO₂ nanoparticles catalyses the liberation of hydrogen from water.^[9] It is also an important factor in the semiconductor industry as the gap width in semiconductors is influenced by the size of metal nanoclusters.^[10]

Experimental

It is sometimes difficult to experimentally measure nucleation rate. The supercooling necessary to get a measurable rate may be at a temperature too low to allow for measurable growth rates. Gustav Tammann developed a method, known as the Tammann or “development” method. ^[11] In this method, crystals are nucleated at a low temperature T_n and then grown at a higher temperature T_g. For validity of this method, the nucleation rate, I, has to be greater at the nucleation temperature T_n than at the growth temperature T_g; I(T_n)>> I(T_g), and the growth rate U must be greater at the growth temperature than at the nucleation temperature T_n ; U(T_g) >> U(T_n). Since the clusters are heated to a larger temperature with a larger critical radius requirement, clusters no longer meet the critical radius requirement and remelt. A method to heat the particles carefully must be used.

Koster proposed a method for nucleation of metallic glasses.^[12] This method considers the sizes of different crystals and attempts to determine when they were formed using data of their growth rates. It can be used for both homogeneous and heterogeneous nucleation.

Footnotes

^ E.M-V. and R. Bowles (2007) Surface nucleation in the freezing of gold nanoparticles. Phys. Rev. Lett. May 4;98 (18) 185503
^ R. J. Young (1981) Introduction to Polymers (CRC Press, NY) ISBN 0-412-22170-5
^ F. F. Abraham (1974) Homogeneous nucleation theory (Academic Press, NY)[Google Books|http://books.google.com/books?id=uftWE2eAH10C&lpg=PA76&dq=homogeneous%20nucleation&pg=PA78#v=onepage&q=homogeneous%20nucleation&f=false]
^ Frank S. Ham (1959) Diffusion-limited growth of precipitate particles, J. Appl. Phys. 30:1518-1525
^ Schmelzer, J (Ed.), Fokin, Yuritsyn, Zanotto. Nucleation Theory and Applications. Nucleation and Crystallization Kinetics in Silicate Glasses: Theory and Experiment. P. 76-83. 2005. Wiley-VCH Verlag GmbH & Co.
^ Mendez-Villuendas E et al. (2007) A limit of stability in supercooled liquid clusters. J Chem Phys. Oct 21;127 (15):154703
^ S.L. Girshick, C.-P. Chiu, The Journal of Chemical Physics 93 (2), pp. 1273-1277 (1990)
^ Anisimov, M.P., Nucleation: theory and experiment. Russian Chemical Reviews, 2003. 72(7): p. 591-600
^ R Palmans, A J Frank J. Phys. Chem. 95 9438 (1991)
^ T Rajh, O I Micic, A J Nozik J. Phys. Chem. 97 11999 (1993)
^ Tammann, Z. Physical Chemistry. B 25, 441. 1898.
^ Schmelzer, J (Ed.), Fokin, Yuritsyn, Zanotto. Nucleation Theory and Applications. Nucleation and Crystallization Kinetics in Silicate Glasses: Theory and Experiment. P. 76-83. 2005. Wiley-VCH Verlag GmbH & Co.

Nucleation

Contents

Examples of nucleation

Mechanics of nucleation

Homogeneous nucleation

Heterogeneous nucleation

Rate of nucleation

The spinodal region

Modern Theory

Classical nucleation

Modifications

Modern technology

Experimental

Footnotes