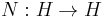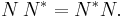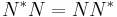Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space  (or equivalently in a C* algebra) is a continuous linear operator
(or equivalently in a C* algebra) is a continuous linear operator
that commutes with its hermitian adjoint N*:
Normal operators are important because the spectral theorem holds for them. Today, the class of normal operators is well-understood. Examples of normal operators are
- unitary operators:
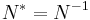
- Hermitian operators (i.e., selfadjoint operators):
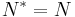 ; (also, anti-selfadjoint operators:
; (also, anti-selfadjoint operators: 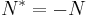 )
) - positive operators:
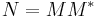
- orthogonal projection operators:
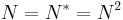
- normal matrices can be seen as normal operators if one takes the Hilbert space to be
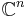 .
.
Contents |
Properties
Normal operators are characterized by the spectral theorem. A compact normal operator (in particular, a normal operator on a finite-dimensional linear space) is diagonalizable.
Let T be a bounded operator. The following are equivalent.
- T is normal.
- T* is normal.
- ||Tx|| = ||T*x|| for all x (use
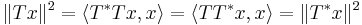 ).
). - The selfadjoint and anti-selfadjoint parts of T commute.
If N is a normal operator, then N and N* have the same kernel and range. Consequently, the range of N is dense if and only if N is injective. Put in another way, the kernel of a normal operator is the orthogonal complement of its range; thus, the kernel of 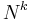 coincides with that of
coincides with that of  for any
for any  . Every generalized eigenvalue of a normal operator is thus genuine.
. Every generalized eigenvalue of a normal operator is thus genuine.  is an eigenvalue of a normal operator N if and only if its complex conjugate
is an eigenvalue of a normal operator N if and only if its complex conjugate 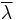 is an eigenvalue of
is an eigenvalue of 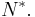 Eigenvectors of a normal operator corresponding to different eigenvalues are orthogonal, and it stabilizes orthogonal complements to its eigenspaces .[1] This implies the usual spectral theorem: every normal operator on a finite-dimensional space is diagonalizable by a unitary operator. There is also an infinite dimensional generalization in terms of projection-valued measures. Residual spectrum of a normal operator is empty.[1]
Eigenvectors of a normal operator corresponding to different eigenvalues are orthogonal, and it stabilizes orthogonal complements to its eigenspaces .[1] This implies the usual spectral theorem: every normal operator on a finite-dimensional space is diagonalizable by a unitary operator. There is also an infinite dimensional generalization in terms of projection-valued measures. Residual spectrum of a normal operator is empty.[1]
The product of normal operators that commute is again normal; this is nontrivial and follows from Fuglede's theorem, which states (in a form generalized by Putnam):
- If
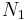 and
and 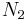 are normal operators and if A is a bounded linear operator such that
are normal operators and if A is a bounded linear operator such that 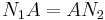 , then
, then 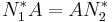 .
.
The operator norm of a normal operator equals to its numerical radius and spectral radius.
A normal operator coincides with its Aluthge transform.
Properties in finite-dimensional case
If a normal operator  on a finite-dimensional real or complex Hilbert space (inner product space)
on a finite-dimensional real or complex Hilbert space (inner product space)  stabilizes a subspace
stabilizes a subspace  , then it also stabilizes its orthogonal complement
, then it also stabilizes its orthogonal complement 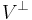 .
.
Proof. Denote by 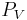 the orthogonal projection onto
the orthogonal projection onto  . Then the orthogonal projection onto
. Then the orthogonal projection onto 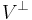 is
is 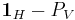 . The fact that
. The fact that  stabilizes
stabilizes  can be expressed as
can be expressed as 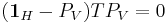 , or
, or 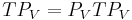 . The goal is to show that
. The goal is to show that 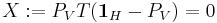 . Since
. Since 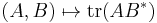 is an inner product on the space of endomorphisms of
is an inner product on the space of endomorphisms of  , it is enough to show that
, it is enough to show that 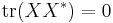 . This follows from a direct computation, using properties of the trace and of orthogonal projections:
. This follows from a direct computation, using properties of the trace and of orthogonal projections:
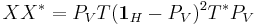
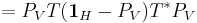
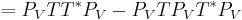 ,
,
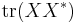
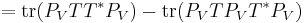
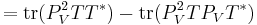
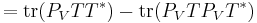
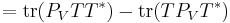
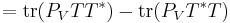
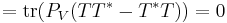 .
.
This generalizes to compact normal operators in infinite dimensional Hilbert spaces.[2] However, for bounded normal operators orthogonal complement to a stable subspace may not be stable.[3] It follows that such subspaces cannot be spanned by eigenvectors.
Normal elements
The notion of normal operators generalizes to an involutive algebra; namely, an element x of an involutive algebra is said to be normal if 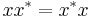 . The most important case is when such an algebra is a C*-algebra. A positive element is an example of a normal element.
. The most important case is when such an algebra is a C*-algebra. A positive element is an example of a normal element.
Unbounded normal operators
The definition of normal operators naturally generalizes to some class of unbounded operators. Explicitly, a closed operator N is said to be normal if
Here, the existence of the adjoint 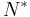 implies that the domain of
implies that the domain of  is dense, and the equality implies that the domain of
is dense, and the equality implies that the domain of 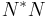 equals that of
equals that of 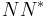 , which is not necessarily the case in general.
, which is not necessarily the case in general.
The spectral theorem still holds for unbounded normal operators, but usually requires a different proof.
Generalization
The success of the theory of normal operators led to several attempts for generalization by weakening the commutativity requirement. Classes of operators that include normal operators are (in order of inclusion)
Notes
- ^ a b Naylor, Arch W.; Sell George R. (1982). Linear Operator Theory in Engineering and Sciences. New York: Springer. ISBN 978-0-387-95001-3. http://books.google.com/books?id=t3SXs4-KrE0C&dq=naylor+sell+linear.
- ^ Andô, Tsuyoshi (1963). "Note on invariant subspaces of a compact normal operator". Archiv der Mathematik 14: 337–340. doi:10.1007/BF01234964.
- ^ Garrett, Paul (2005). "Operators on Hilbert spaces". http://www.math.umn.edu/~garrett/m/fun/Notes/04a_ops_hsp.pdf.