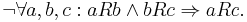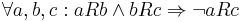Intransitivity
In mathematics, the term intransitivity is used for related, but different, properties of binary relations:
Contents |
Intransitivity
A relation is transitive if, whenever it relates some A to some B, and that B to some C, it also relates that A to that C. Some authors call a relation intransitive if it is not transitive, i.e.
Where  indicates some relationship.
indicates some relationship.
For instance, in the food chain, wolves feed on deer, and deer feed on grass, but wolves do not feed on grass.[1] Thus, the feed on relation among life forms is intransitive, in this sense.
Another example that does not involve preference loops arises in freemasonry: it may be the case that lodge A recognizes lodge B, and lodge B recognizes lodge C, but lodge A does not recognize lodge C. Thus the recognition relation among Masonic lodges is intransitive.
Antitransitivity
Often the term intransitive is used to refer to the stronger property of antitransitivity.
We just saw that the feed on relation is not transitive, but it still contains some transitivity: for instance: humans feed on rabbits, rabbits feed on carrots, and humans also feed on carrots.
A relation is antitransitive if this never occurs at all, i.e.,
Many authors use the term intransitivity to mean antitransitivity.[2][3]
An example of an antitransitive relation: the defeated relation in knockout tournaments. If player A defeated player B and player B defeated player C, A can have never played C, and therefore, A has not defeated C.
Cycles
The term intransitivity is often used when speaking of scenarios in which a relation describes the relative preferences between pairs of options, and weighing several options produces a "loop" of preference:
- A is preferred to B
- B is preferred to C
- C is preferred to A
Rock, paper, scissors is an example.
Assuming no option is preferred to itself i.e. the relation is irreflexive, a preference relation with a loop is not transitive. For if it is, each option in the loop is preferred to each option, including itself. This can be illustrated for this example of a loop among A, B, and C. Assume the relation is transitive. Then, since A is preferred to B and B is preferred to C, also A is preferred to C. But then, since C is preferred to A, also A is preferred to A.
Therefore such a preference loop (or "cycle") is known as an intransitivity.
Notice that a cycle is neither necessary nor sufficient for a binary relation to be not transitive. For example, an equivalence relation possesses cycles but is transitive. Now, consider the relation "is an enemy of" and suppose that the relation is symmetric and satisfies the condition that for any country, any enemy of an enemy of the country is not itself an enemy of the country. This is an example of an antitransitive relation that does not have any cycles. In particular, by virtue of being antitransitive the relation is not transitive.
Finally, let us work with the example of rock, paper, scissors, calling the three options A, B, and C. Now, the relation over A, B, and C is "defeats" and the standard rules of the game are such that A defeats B, B defeats C, and C defeats A. Furthermore, it is also true that B does not defeat A, C does not defeat B, and A does not defeat C. Finally, it is also true that no option defeats itself. This information can be depicted in a table:
| A | B | C | |
|---|---|---|---|
| A | 0 | 1 | 0 |
| B | 0 | 0 | 1 |
| C | 1 | 0 | 0 |
The first argument of the relation is a row and the second one is a column. Ones indicate the relation holds, zero indicates that it does not hold. Now, notice that the following statement is true for any pair of elements x and y drawn (with replacement) from the set {A, B, C}: If x defeats y, and y defeats z, then x does not defeat z. Hence the relation is antitransitive.
Thus, a cycle is neither necessary nor sufficient for a binary relation to be antitransitive.
Occurrences in preferences
- Intransitivity can occur under majority rule, in probabilistic outcomes of game theory, and in the Condorcet voting method in which ranking several candidates can produce a loop of preference when the weights are compared (see voting paradox). Intransitive dice demonstrate that probabilities are not necessarily transitive.
- In psychology, intransitivity often occurs in a person's system of values (or preferences, or tastes), potentially leading to unresolvable conflicts.
- Analogously, in economics intransitivity can occur in a consumer's preferences. This may lead to consumer behaviour that does not conform to perfect economic rationality. In recent years, economists and philosophers have questioned whether violations of transitivity must necessarily lead to 'irrational behaviour' (see Anand (1993)).
Likelihood
It has been suggested that Condorcet voting tends to eliminate "intransitive loops" when large numbers of voters participate because the overall assessment criteria for voters balances out. For instance, voters may prefer candidates on several different units of measure such as by order of social consciousness or by order of most fiscally conservative.
In such cases intransitivity reduces to a broader equation of numbers of people and the weights of their units of measure in assessing candidates.
Such as:
- 30% favor 60/40 weighting between social consciousness and fiscal conservatism
- 50% favor 50/50 weighting between social consciousness and fiscal conservatism
- 20% favor a 40/60 weighting between social consciousness and fiscal conservatism
While each voter may not assess the units of measure identically, the trend then becomes a single vector on which the consensus agrees is a preferred balance of candidate criteria.
References
- ^ Wolves do eat grass - see Engel, Cindy (2003). Wild Health: Lessons in Natural Wellness from the Animal Kingdom (paperback ed.). Houghton Mifflin. p. 141. ISBN 0-618-34068-8..
- ^ Guide to Logic, Relations II
- ^ IntransitiveRelation
Further reading
- Anand, P (1993). Foundations of Rational Choice Under Risk. Oxford: Oxford University Press..