Noncototient
In mathematics, a noncototient is a positive integer n that cannot be expressed as the difference between a positive integer m and the number of coprime integers below it. That is, m − φ(m) = n, where φ stands for Euler's totient function, has no solution for m. The cototient of n is defined as n − φ(n), so a noncototient is a number that is never a cototient.
It is conjectured that all noncototients are even. This follows from a modified form of the Goldbach conjecture: if the even number n can be represented as a sum of two distinct primes p and q, then
It is expected that every even number larger than 6 is a sum of distinct primes, so probably no odd number larger than 5 is a noncototient. The remaining odd numbers are covered by the observations 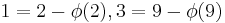 and
and 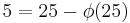 .
.
The first few noncototients are:
10, 26, 34, 50, 52, 58, 86, 100, 116, 122, 130, 134, 146, 154, 170, 172, 186, 202, 206, 218, 222, 232, 244, 260, 266, 268, 274, 290, 292, 298, 310, 326, 340, 344, 346, 362, 366, 372, 386, 394, 404, 412, 436, 466, 470, 474, 482, 490, 518, 520 (sequence A005278 in OEIS)
Erdős and Sierpinski asked whether there exist infinitely many noncototients. This was finally answered in the affirmative by Browkin and Schinzel (1995), who showed every member of the infinite family 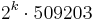 is an example. Since then other infinite families, of roughly the same form, have been given by Flammenkamp and Luca.
is an example. Since then other infinite families, of roughly the same form, have been given by Flammenkamp and Luca.
External links
|
|||||
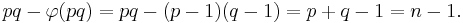
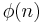 ·
·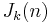 ·
·