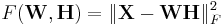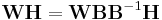Non-negative matrix factorization

NMF redirects here. For the bridge convention, see new minor forcing.

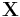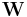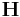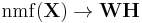
Non-negative matrix factorization (NMF) is a group of algorithms in multivariate analysis and linear algebra where a matrix, \mathbf{X}, is factorized into (usually) two matrices, \mathbf{W} and \mathbf{H} : \operatorname{nmf}(\mathbf{X}) \rightarrow \mathbf{WH}

Factorization of matrices is generally non-unique, and a number of different methods of doing so have been developed (e.g. principal component analysis and singular value decomposition) by incorporating different constraints; non-negative matrix factorization differs from these methods in that it enforces the constraint that the factors W and H must be non-negative, i.e., all elements must be equal to or greater than zero.

Contents

History

In chemometrics non-negative matrix factorization has a long history under the name "self modeling curve resolution".[1] In this framework the vectors in the right matrix are continuous curves rather than discrete vectors. Also early work on non-negative matrix factorizations was performed by a Finnish group of researchers in the middle of the 1990s under the name positive matrix factorization.[2][3] It became more widely known as non-negative matrix factorization after Lee and Seung investigated the properties of the algorithm and published some simple and useful algorithms for two types of factorizations.[4][5]

Types

Approximative non-negative matrix factorization

Usually the number of columns of W and the number of rows of H in NMF are selected so the product WH will become an approximation to X (it has been suggested that the NMF model should be called nonnegative matrix approximation instead). The full decomposition of X then amounts to the two non-negative matrices W and H as well as a residual U, such that: X = WH + U. The elements of the residual matrix can either be negative or positive.

When W and H are smaller than X they become easier to store and manipulate.

Different cost functions and regularizations

There are different types of non-negative matrix factorizations. The different types arise from using different cost functions for measuring the divergence between X and WH and possibly by regularization of the W and/or H matrices.[6]

Two simple divergence functions studied by Lee and Seung are the squared error (or Frobenius norm) and an extension of the Kullback-Leibler divergence to positive matrices (the original Kullback-Leibler divergence is defined on probability distributions). Each divergence leads to a different NMF algorithm, usually minimizing the divergence using iterative update rules.

The factorization problem in the squared error version of NMF may be stated as: Given a matrix 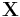\mathbf{X} find nonnegative matrices W and H that minimize the function

F(\mathbf{W},\mathbf{H}) = \|\mathbf{X} - \mathbf{WH}\|^2_F

Another type of NMF for images is based on the total variation norm.[7]

Algorithms

There are several ways in which the W and H may be found: Lee and Seung's updates are usually referred to as the multiplicative update method, while others have suggested gradient descent algorithms and so-called alternating non-negative least squares and "projected gradient".[8][9]

The currently available algorithms are sub-optimal as they can only guarantee finding a local minima, rather than a global minimum of the cost function. A provably optimal algorithm is unlikely in the near future as the problem has been shown to generalize the k-means clustering problem which is known to be computationally difficult (NP-complete)[10]. However, as in many other data mining applications a local minimum may still prove to be useful.

Relation to other techniques

In Learning the parts of objects by non-negative matrix factorization Lee and Seung proposed NMF mainly for parts-based decomposition of images. It compares NMF to vector quantization and principal component analysis, and shows that although the three techniques may be written as factorizations, they implement different constraints and therefore produce different results.

It was later shown that some types of NMF are an instance of a more general probabilistic model called "multinomial PCA".[11] When NMF is obtained by minimizing the Kullback–Leibler divergence, it is in fact equivalent to another instance of multinomial PCA, probabilistic latent semantic analysis,[12] trained by maximum likelihood estimation. That method is commonly used for analyzing and clustering textual data and is also related to the latent class model.

It has been shown [13][14] NMF is equivalent to a relaxed form of K-means clustering: matrix factor W contains cluster centroids and H contains cluster membership indicators, when using the least square as NMF objective. This provides theoretical foundation for using NMF for data clustering.

When using KL divergence as the objective function, it is shown [15] that NMF has a Chi-square interpretation and is equivalent to probabilistic latent semantic analysis.

NMF extends beyond matrices to tensors of arbitrary order.[16][17] This extension may be viewed as a non-negative version of, e.g., the PARAFAC model.

NMF is an instance of the nonnegative quadratic programming (NQP) as well as many other important problems including the support vector machine (SVM). However, SVM and NMF are related at a more intimate level than that of NQP, which allows direct application of the solution algorithms developed for either of the two methods to problems in both domains.[18]

Uniqueness

The factorization is not unique: A matrix and its inverse can be used to transform the two factorization matrices by, e.g.,[19]

\mathbf{WH} = \mathbf{WBB}^{-1}\mathbf{H}

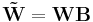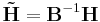If the two new matrices \mathbf{\tilde{W} = WB} and \mathbf{\tilde{H}}=\mathbf{B}^{-1}\mathbf{H} are non-negative they form another parametrization of the factorization.

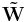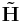The non-negativity of \mathbf{\tilde{W}} and \mathbf{\tilde{H}} applies at least if B is a non-negative monomial matrix. In this simple case it will just correspond to a scaling and a permutation.

More control over the non-uniqueness of NMF is obtained with sparsity constraints.[20]

Applications

Text mining

NMF can be used for text mining applications. In this process, a document-term matrix is constructed with the weights of various terms (typically weighted word frequency information) from a set of documents. This matrix is factored into a term-feature and a feature-document matrix. The features are derived from the contents of the documents, and the feature-document matrix describes data clusters of related documents.

One specific application used hierarchical NMF on a small subset of scientific abstracts from PubMed.[21] Another research group clustered parts of the Enron email dataset[22] with 65,033 messages and 91,133 terms into 50 clusters.[23] NMF has also been applied to citations data, with one example clustering Wikipedia articles and scientific journals based on the outbound scientific citations in Wikipedia.[24]

Spectral data analysis

NMF is also used to analyze spectral data; one such use is in the classification of space objects and debris.[25]

Scalable Internet distance prediction

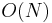NMF is applied in scalable Internet distance (round-trip time) prediction. For a network with N hosts, with the help of NMF, the distances of all the N^2 end-to-end links can be predicted by conduct only O(N) measurements. This kind of method was firstly introduced in Internet Distance Estimation Service (IDES).[26] Afterwards, as a fully decentralized approach, Phoenix network coordinate system [27] is proposed. It achieves better overall prediction accuracy by introducing the concept of weight.

Non-stationary Speech Denoising

Speech denoising has been a long lasting problem in audio processing community. There exist lots of algorithms for denoising is the noise is stationary. For example, Wiener filter is suitable for additive Gaussian noise. However, if the noise is non-stationary, the classical denoising algorithms usually have poor performance because the statistical information of the non-stationary noise is difficult to estimate. Schmidt [28] use NMF do speech denoising under non-stationary noise, which is completely different than classical statistical approaches.The key idea is that clean speech signal can be sparsely represented by a speech dictionary, but non-stationary noise cannot. Similarly, non-stationary noise can also be sparsely represented by a noise dictionary, but speech cannot.

The algorithm for NMF denoising goes as follows. Two dictionaries, one for speech and one for noise, need to be trained offline. Once a noisy speech is given, we first calculate the magnitude of the Short-Time-Fourier-Transform. Second, separate it into two parts via NMF, one can be sparsely represented by the speech dictionary, and the other part can be sparsely represented by the noise dictionary. Third, the part that is represented by the dictionary will be the estimated clean speech.

Current research

Current research in nonnegative matrix factorization includes, but not limited to,

(1) Algorithmic: searching for global minima of the factors and factor initialization.[29]

(2) Scalability: how to factorize million-by-billion matrices, which are commonplace in Web-scale data mining, e.g., see Distributed Nonnegative Matrix Factorization (DNMF)[30]

(3) Online: how to update the factorization when new data comes in without recomputing from scratch.

See also

Sources and external links

Notes

  1. ^ William H. Lawton; Edward A. Sylvestre (August 1971). "Self modeling curve resolution". Technometrics 13 (3): 617+. 
  2. ^ P. Paatero, U. Tapper (1994). "Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values". Environmetrics 5 (2): 111–126. doi:10.1002/env.3170050203. 
  3. ^ Pia Anttila, Pentti Paatero, Unto Tapper, Olli Järvinen (1995). "Source identification of bulk wet deposition in Finland by positive matrix factorization". Atmospheric Environment 29 (14): 1705–1718. doi:10.1016/1352-2310(94)00367-T. 
  4. ^ Daniel D. Lee and H. Sebastian Seung (1999). "Learning the parts of objects by non-negative matrix factorization". Nature 401 (6755): 788–791. doi:10.1038/44565. PMID 10548103. 
  5. ^ Daniel D. Lee and H. Sebastian Seung (2001). "Algorithms for Non-negative Matrix Factorization". Advances in Neural Information Processing Systems 13: Proceedings of the 2000 Conference. MIT Press. pp. 556–562. http://www.nips.cc/Web/Groups/NIPS/NIPS2000/00papers-pub-on-web/LeeSeung.ps.gz. 
  6. ^ Inderjit S. Dhillon, Suvrit Sra (2005). "Generalized Nonnegative Matrix Approximations with Bregman Divergences" (PDF). NIPS. http://books.nips.cc/papers/files/nips18/NIPS2005_0203.pdf. 
  7. ^ Taiping Zhanga, Bin Fang, Weining Liu, Yuan Yan Tang, Guanghui He and Jing Wen (June 2008). "Total variation norm-based nonnegative matrix factorization for identifying discriminant representation of image patterns". Neurocomputing 71 (10–12): 1824–1831. doi:10.1016/j.neucom.2008.01.022. 
  8. ^ Chih-Jen Lin (October 2007). "Projected Gradient Methods for Non-negative Matrix Factorization" (PDF). Neural Computation 19 (10). http://www.csie.ntu.edu.tw/~cjlin/papers/pgradnmf.pdf. 
  9. ^ Chih-Jen Lin (November 2007). "On the Convergence of Multiplicative Update Algorithms for Nonnegative Matrix Factorization". IEEE Transactions on Neural Networks 18 (6): 1589–1596. doi:10.1109/TNN.2007.895831. 
  10. ^ Ding, C. and He, X. and Simon, H.D., (2005). "On the equivalence of nonnegative matrix factorization and spectral clustering". Proc. SIAM Data Mining Conf 4: 606–610. 
  11. ^ Wray Buntine (2002). "Variational Extensions to EM and Multinomial PCA" (PDF). Proc. European Conference on Machine Learning (ECML-02). LNAI. 2430. pp. 23–34. http://cosco.hiit.fi/Articles/ecml02.pdf. 
  12. ^ Eric Gaussier and Cyril Goutte (2005). "Relation between PLSA and NMF and Implications" (PDF). Proc. 28th international ACM SIGIR conference on Research and development in information retrieval (SIGIR-05). pp. 601–602. http://eprints.pascal-network.org/archive/00000971/01/39-gaussier.pdf. 
  13. ^ Chris Ding, Xiaofeng He, and Horst D. Simon (2005). "On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering". Proc. SIAM Int'l Conf. Data Mining, pp. 606-610. May 2005
  14. ^ Ron Zass and Amnon Shashua (2005). "A Unifying Approach to Hard and Probabilistic Clustering". International Conference on Computer Vision (ICCV) Beijing, China, Oct., 2005.
  15. ^ Chris Ding, Tao Li, Wei Peng (2006). "Nonnegative Matrix Factorization and Probabilistic Latent Semantic Indexing: Equivalence Chi-Square Statistic, and a Hybrid Method. AAAI 2006
  16. ^ Pentti Paatero (1999). "The Multilinear Engine: A Table-Driven, Least Squares Program for Solving Multilinear Problems, including the n-Way Parallel Factor Analysis Model". Journal of Computational and Graphical Statistics 8 (4): 854–888. doi:10.2307/1390831. JSTOR 1390831. 
  17. ^ Max Welling and Markus Weber (2001). "Positive Tensor Factorization". Pattern Recognition Letters 22 (12): 1255–1261. doi:10.1016/S0167-8655(01)00070-8. 
  18. ^ Vamsi K. Potluru and Sergey M. Plis and Morten Morup and Vince D. Calhoun and Terran Lane (2009). "Efficient Multiplicative updates for Support Vector Machines". Proceedings of the 2009 SIAM Conference on Data Mining (SDM). pp. 1218–1229. 
  19. ^ Wei Xu, Xin Liu & Yihong Gong (2003). "Document clustering based on non-negative matrix factorization". Proceedings of the 26th annual international ACM SIGIR conference on Research and development in informaion retrieval. New York: Association for Computing Machinery. pp. 267–273. http://portal.acm.org/citation.cfm?id=860485. 
  20. ^ Julian Eggert, Edgar Körner, "Sparse coding and NMF", Proceedings. 2004 IEEE International Joint Conference on Neural Networks, 2004., pp. 2529-2533, 2004.
  21. ^ Nielsen, Finn Årup; Balslev, Daniela; Hansen, Lars Kai (September 2005). "Mining the posterior cingulate: segregation between memory and pain components". NeuroImage 27 (3): 520–522. doi:10.1016/j.neuroimage.2005.04.034. PMID 15946864. 
  22. ^ Cohen, William (2005-04-04). "Enron Email Dataset". http://www.cs.cmu.edu/~enron/. Retrieved 2008-08-26. 
  23. ^ Berry, Michael W.; Browne, Murray (October 2005). "Email Surveillance Using Non-negative Matrix Factorization". Computational and Mathematical Organization Theory 11 (3): 249–264. doi:10.1007/s10588-005-5380-5. 
  24. ^ Nielsen, Finn Årup (2008). "Clustering of scientific citations in Wikipedia". Wikimania. http://www2.imm.dtu.dk/pubdb/views/publication_details.php?id=5666. 
  25. ^ Michael W. Berry, et al. (June 2006). Algorithms and Applications for Approximate Nonnegative Matrix Factorization. 
  26. ^ Yun Mao, Lawrence Saul and Jonathan M. Smith (December 2006). "IDES: An Internet Distance Estimation Service for Large Networks". IEEE Journal on Selected Areas in Communications 24 (12): 2273–2284. doi:10.1109/JSAC.2006.884026. 
  27. ^ Yang Chen, Xiao Wang, Cong Shi, and et al. (December 2011). "Phoenix: A Weight-based Network Coordinate System Using Matrix Factorization" (PDF). IEEE Transactions on Network and Service Management 8 (4): 334-347. http://www.cs.duke.edu/~ychen/Phoenix_TNSM.pdf. 
  28. ^ Schmidt, M.N., J. Larsen, and F.T. Hsiao. 2007. Wind noise reduction using non-negative sparse coding. In Machine Learning for Signal Processing, 2007 IEEE Workshop on, 431–436
  29. ^ C. Boutsidis and E. Gallopoulos (April 2008). "SVD based initialization: A head start for nonnegative matrix factorization". Pattern Recognition 41 (4): 1350–1362. doi:10.1016/j.patcog.2007.09.010. 
  30. ^ Chao Liu, Hung-chih Yang, Jinliang Fan, Li-Wei He, and Yi-Min Wang (April 2010). "Distributed Nonnegative Matrix Factorization for Web-Scale Dyadic Data Analysis on MapReduce". Proceedings of the 19th International World Wide Web Conference. http://research.microsoft.com/pubs/119077/DNMF.pdf. 

Others

Software