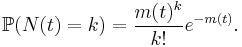Non-homogeneous Poisson process
In probability theory, a non-homogeneous Poisson process is a Poisson process with rate parameter 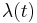 such that the rate parameter of the process is a function of time.[1] Non-homogeneous Poisson process have been shown to describe numerous random phenomena[2] including cyclone prediction[3], arrival times of calls to a call centre in a hospital laboratory,[4] arrival times of aircraft to airspace around an airport[5] and database transaction times.[6]
such that the rate parameter of the process is a function of time.[1] Non-homogeneous Poisson process have been shown to describe numerous random phenomena[2] including cyclone prediction[3], arrival times of calls to a call centre in a hospital laboratory,[4] arrival times of aircraft to airspace around an airport[5] and database transaction times.[6]
Contents |
Definition
Write N(t) for the number of events by time t. A stochastic process is a non-homogeneous Poisson process for some small value h if:[7][1]
- N(0)=0
- Non-overlapping increments are independent
- P(N(t+h)-N(t)=1) = λ(t)h + o(h)
- P(N(t+h)-N(t)>1) = o(h)
for all t and where, in big O notation, 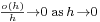 .
.
Properties
Write N(t) for the number of events by time t and 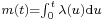 for the mean. Then N(t) has a Poisson distribution with mean m(t), that is for k = 0, 1, 2, 3….[8]
for the mean. Then N(t) has a Poisson distribution with mean m(t), that is for k = 0, 1, 2, 3….[8]
Simulation
To simulate a non-homogeneous Poisson process with intensity function λ(t), choose a sufficiently large λ so that λ(t) = λ p(t) and simulate a Poisson process with rate parameter λ. Accept an event from the Poisson simulation at time t with probability p(t).[1]
See also
- Cox process, where λ(t) can be a stochastic process.
Notes
- ^ a b c Ross, Sheldon M. (2006). Simulation. Academic Press. p. 32. ISBN 0125980639.
- ^ Leemis, Larry (May 2003). "Estimating and Simulating Nonhomogeneous Poisson Processes". William and Mary Mathematics Department. http://www.math.wm.edu/~leemis/icrsa03.pdf. Retrieved Sep 26 2011.
- ^ Lee, Sanghoon; Wilson, James R.; Crawford, Melba M. (1991). "Modeling and simulation of a nonhomogeneous poisson process having cyclic behavior". Communications in Statistics - Simulation and Computation 20 (2-3): 777–809. doi:10.1080/03610919108812984. http://www.ise.ncsu.edu/jwilson/files/lee91.pdf.
- ^ Kao, Edward P. C.; Chang, Sheng-Lin (November 1988). "Modeling Time-Dependent Arrivals to Service Systems: A Case in Using a Piecewise-Polynomial Rate Function in a Nonhomogeneous Poisson Process". Management Science (INFORMS) 34 (11): 1367–1379. doi:10.1287/mnsc.34.11.1367. JSTOR 2631999.
- ^ Galliher, Herbert P.; Wheeler, R. Clyde (March-April 1958). "Nonstationary Queuing Probabilities for Landing Congestion of Aircraft". Operations Research 6 (2): 264–275. doi:10.1287/opre.6.2.264. JSTOR 167618.
- ^ Lewis, P. A. W.; Shedler, G. S. (September 1976). "Statistical Analysis of Non-stationary Series of Events in a Data Base System". IBM Journal of Research and Development 20 (5). doi:10.1147/rd.205.0465. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.84.9018&rep=rep1&type=pdf.
- ^ Srinivasan (1974). "Chapter 2". Stochastic point processes and their applications. ISBN 0852642237.
- ^ Pham, Hoang (2006). System software reliability. Springer. p. 176. ISBN 1852339500.