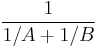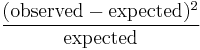Nomogram
- This article is about the graphical devices called nomograms. Not to be confused with nonograms, a kind of Japanese puzzle, or monograms, small motifs of combined letters.
A nomogram, nomograph, or abac is a graphical calculating device developed by P.E. Elyasberg[1], a two-dimensional diagram designed to allow the approximate graphical computation of a function: it uses a coordinate system other than Cartesian coordinates. Defining alternatively, a nomogram is a (two-dimensionally) plotted function with n parameters, from which, knowing n-1 parameters, the unknown one can be read, or fixing some parameters, the relationship between the unfixed ones can be studied. Like a slide rule, it is a graphical analog computation device; and, like the slide rule, its accuracy is limited by the precision with which physical markings can be drawn, reproduced, viewed, and aligned. Most nomograms are used in applications where an approximate answer is appropriate and useful. Otherwise, the nomogram may be used to check an answer obtained from an exact calculation method.
The slide rule is intended to be a general-purpose device. Nomograms are usually designed to perform a specific calculation, with tables of values effectively built in to the construction of the scales.
Contents |
Description
A nomogram typically has three scales: two scales represent known values and one scale is the scale where the result is read off. The known scales are placed on the outside; i.e. the result scale is in the center. Each known value of the calculation is marked on the outer scales and a line is drawn between each mark. Where the line and the inside scale intersects is the result. The scale marks include 'tick marks' to indicate exact number locations, and labeled reference values. These scales may be linear, logarithmic or have some more complex relationship. Straight scales are useful for relatively simple calculations, but for more complex calculations, simple or elaborate curved scales may need to be used.
Using a nomogram is simple — a taut string or other straight edge is placed so as to contact the two known values on their lines. The required answer is read off another line. This allows calculation of one variable when the other two are known. Additional lines are sometimes added that are simple conversions of one of the other variables.
Examples
- The Smith chart (see figure at the top), used in electronics and systems analysis.
- Thermodynamic diagrams and tephigrams, used to plot the vertical structure of the atmosphere and perform calculations on its stability and humidity content.
Parallel-resistance/thin-lens nomogram
The nomogram below performs the computation
This nomogram is interesting because it performs a useful nonlinear calculation using only straight-line, equally-graduated scales.
A and B are entered on the horizontal and vertical scales, and the result is read from the diagonal scale. Being proportional to the harmonic mean of A and B, this formula has several applications. For example, it is the parallel-resistance formula in electronics, and the thin-lens equation in optics.
In the example below, the red line demonstrates that parallel resistors of 56 and 42 ohms have a combined resistance of 24 ohms. It also demonstrates that an object at a distance of 56 cm from a lens whose focal length is 24 cm forms a real image at a distance of 42 cm.
Chi-squared test computation nomogram
The nomogram below can be used to perform an approximate computation of some values needed when performing a familiar statistical test, Pearson's chi-squared test. This nomogram demonstrates the use of curved scales with unevenly-spaced graduations.
The relevant expression is
The blue line demonstrates the computation of
- (9 − 5)2/ 5 = 3.2
The red line demonstrates the computation of
- (81 − 70)2 / 70 = 1.7
In performing the test, Yates's correction for continuity is often applied, and simply involves subtracting 0.5 from the observed values. A nomogram for performing the test with Yates's correction could be constructed simply by shifting each "observed" scale half a unit to the left, so that the 1.0, 2.0, 3.0, ... graduations are placed where the values 0.5, 1.5, 2.5, ... appear on the present chart.
Food risk assessment nomogram
Although nomograms represent mathematical relationships, not all are mathematically derived. The following one was developed from the graphical end to achieve appropriate end results that could readily be defined by the product of their relationships in subjective units rather than numerically. The use of non-parallel axes enabled the non-linear relationships to be incorporated in the model.
The numbers in square boxes denote the axes requiring input after appropriate assessment.
The pair of nomograms at the top of the image determine the probability of occurrence, and the availability, which are then incorporated in the bottom multistage nomogram.
Lines 8 and 10 are ‘tie lines’ for the transition between the stages of the nomogram.
The final pair of parallel logarithmic scales (12) are not nomograms as such, but reading-off scales to translate the risk score (11, remote to extremely high) into a sampling frequency to address safety aspects and other ‘consumer protection’ aspects respectively. This stage requires political ‘buy in’ balancing cost against risk. The example uses a 3 year minimum frequency for each, though with the high risk end of the scales different for the two aspects, giving different frequencies for the two, but both subject to an overall minimum sampling of every food for all aspects at least once every three years.
This risk assessment nomogram was developed by the UK Public Analyst Service with funding from the UK Food Standards Agency for use as a tool to guide the appropriate frequency of sampling & analysis of food for official food control purposes, intended to be used to assess all potential problems with all foods, although not yet adopted.
See also
References
- M. d'Ocagne: "Traité de Nomographie", Gauthier-Villars, Paris, 1899.
- M. d'Ocagne: "Sur la résolution nomographique de l'équation du septième degré." Comptes rendus Paris, 131 (1900), 522–524.
External links
- Weisstein, Eric W., "Nomogram" from MathWorld.
- The Art of Nomography describes the design of nomograms using geometry, determinants, and transformations.
- The Lost Art of Nomography is a math journal article surveying the field of nomography.
- Nomograms for Wargames but also of general interest.
- Java Applet for constructing simple nomograms.
- Nomograms for visualising relationships between three variables - invited talk by Jonathan Rougier for useR! 2011.