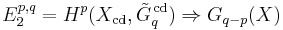Nisnevich topology

In algebraic geometry, the Nisnevich topology, sometimes called the completely decomposed topology, is a Grothendieck topology on the category of schemes which has been used in algebraic K-theory, A¹ homotopy theory, and the theory of motives. It was originally introduced by Yevsey Nisnevich, who was motivated by the theory of adeles.

Contents

Definition

A morphism of schemes f : Y → X is called a Nisnevich morphism if it is an étale morphism such that for every (possibly non-closed) point x ∈ X, there exists a point y ∈ Y such that the induced map of residue fields k(x) → k(y) is an isomorphism. Equivalently, f must be flat, unramified, locally of finite presentation, and for every point x ∈ X, there must exist a point y in the fiber f−1(x) such that k(x) → k(y) is an isomorphism.

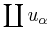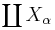A family of morphisms {uα : Xα → X} is a Nisnevich cover if each morphism in the family is étale and for every (possibly non-closed) point x ∈ X, there exists α and a point y ∈ Xα s.t. uα(y) = x and the induced map of residue fields k(x) → k(y) is an isomorphism. If the family is finite, this is equivalent to the morphism \coprod u_\alpha from \coprod X_\alpha to X being a Nisnevich morphism. The Nisnevich covers are the covering families of a pretopology on the category of schemes and morphisms of schemes. This generates a topology called the Nisnevich topology. The category of schemes with the Nisnevich topology is notated Nis.

The small Nisnevich site of X is the category O(XNis) whose objects are schemes U with a fixed Nisnevich morphism U → X. The morphisms are morphisms of schemes compatible with the fixed maps to X. The big Nisnevich site of X is the category Nis/X, that is, the category of schemes with a fixed map to X, considered with the Nisnevich topology.

The Nisnevich topology has several variants which are adapted to studying singular varieties. Covers in these topologies include resolutions of singularities or weaker forms of resolution.

The cdh and l′ topologies are incomparable with the étale topology, and the qfh topology is finer than the étale topology.

Local rings in the Nisnevich topology

See also: Henselian ring

If x is a point of a scheme X, then the local ring of x in the Nisnevich topology is the henselization of the local ring of x in the Zariski topology.

Applications

Nisnevich introduced his topology to provide a cohomological interpretation of the class set of an affine group scheme, which was originally defined in adelic terms. He used it to partially prove a conjecture of Alexander Grothendieck and Jean-Pierre Serre which states that a rationally trivial torsor is locally trivial in the Zariski topology. One of the key properties of the Nisnevich topology is the existence of a descent spectral sequence. Let X be a Noetherian scheme of finite Krull dimension. Let Gn(X) denote the Quillen K-groups of the category of coherent sheaves on X, and let 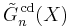\tilde G_n^{\,\text{cd}}(X) denote the sheavings of these groups with respect to the Nisnevich topology. Then there is a convergent spectral sequence

E^{p,q}_2 = H^p(X_\text{cd}, \tilde G_q^{\,\text{cd}}) \Rightarrow G_{q-p}(X)

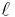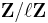for p ≥ 0, q ≥ 0, and p - q ≥ 0. If \ell is a prime number not equal to the characteristic of X, then there is an analogous convergent spectral sequence for K-groups with coefficients in \mathbf{Z}/\ell\mathbf{Z}.

The Nisnevich topology has also found important applications in algebraic K-theory, A¹ homotopy theory and the theory of motives.

References