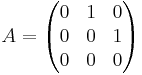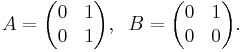Nilpotent

In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xⁿ = 0.

The term was introduced by Benjamin Peirce^[1] in the context of elements of an algebra that vanish when raised to a power.

1 Examples
2 Properties
3 Nilpotency in physics
4 Algebraic nilpotents
5 See also
6 References

Examples

This definition can be applied in particular to square matrices. The matrix

$A = \begin{pmatrix} 0&1&0\\ 0&0&1\\ 0&0&0\end{pmatrix}$

is nilpotent because A³ = 0. See nilpotent matrix for more.

In the factor ring Z/9Z, the equivalence class of 3 is nilpotent because 3² is congruent to 0 modulo 9.

Assume that two elements a, b in a (non-commutative) ring R satisfy ab = 0. Then the element c = ba is nilpotent (if non-zero) as c² = (ba)² = b(ab)a = 0. An example with matrices (for a, b):

$A = \begin{pmatrix} 0&1\\ 0&1 \end{pmatrix}, \;\; B =\begin{pmatrix} 0&1\\ 0&0 \end{pmatrix}.$

Here AB = 0, BA = B.

The ring of coquaternions contains a cone of nilpotents.

Properties

No nilpotent element can be a unit (except in the trivial ring {0} which has only a single element 0 = 1). All non-zero nilpotent elements are zero divisors.

An n-by-n matrix A with entries from a field is nilpotent if and only if its characteristic polynomial is tⁿ.

The nilpotent elements from a commutative ring form an ideal; this is a consequence of the binomial theorem. This ideal is the nilradical of the ring. Every nilpotent element in a commutative ring is contained in every prime ideal of that ring, and in fact the intersection of all these prime ideals is equal to the nilradical.

If x is nilpotent, then 1 − x is a unit, because xⁿ = 0 entails

$(1 - x) (1 %2B x %2B x^2 %2B \cdots %2B x^{n-1}) = 1 - x^n = 1.\$

Further, if x is nilpotent, then 1 + x is also a unit.^[2]

Nilpotency in physics

An operand Q that satisfies Q² = 0 is nilpotent. Grassmann numbers which allow a path integral representation for Fermionic fields are nilpotents since their squares vanish. The BRST charge is an important example in physics. As linear operators form an associative algebra and thus a ring, this is a special case of the initial definition.^[3]^[4] More generally, in view of the above definitions, an operator Q is nilpotent if there is n∈N such that Qⁿ = 0 (the zero function). Thus, a linear map is nilpotent iff it has a nilpotent matrix in some basis. Another example for this is the exterior derivative (again with n = 2). Both are linked, also through supersymmetry and Morse theory^[5], as shown by Edward Witten in a celebrated article.^[6]

The electromagnetic field of a plane wave without sources is nilpotent when it is expressed in terms of the algebra of physical space.^[7]

Algebraic nilpotents

The two-dimensional dual numbers contain a nilpotent basis element. Other algebras and numbers that contain nilpotent spaces include split-quaternions (coquaternions), split-octonions, biquaternions 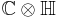$\mathbb C\otimes\mathbb H$ , and complex octonions $\mathbb C\otimes\mathbb O$ .

References

^ Polcino & Sehgal (2002), p. 127.
^ see Planetmath
^ Peirce, B. Linear Associative Algebra. 1870.
^ Milies, César Polcino; Sehgal, Sudarshan K. An introduction to group rings. Algebras and applications, Volume 1. Springer, 2002. ISBN 9781402002380
^ A. Rogers, The topological particle and Morse theory, Class. Quantum Grav. 17:3703–3714,2000 doi:10.1088/0264-9381/17/18/309.
^ E Witten, Supersymmetry and Morse theory. J.Diff.Geom.17:661–692,1982.
^ Rowlands, P. Zero to Infinity: The Foundations of Physics, London, World Scientific 2007, ISBN 978-981-270-914-1