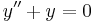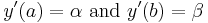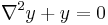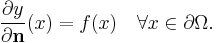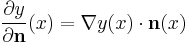Neumann boundary condition

In mathematics, the Neumann (or second-type) boundary condition is a type of boundary condition, named after Carl Neumann.^[1] When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.

For an ordinary differential equation, for instance:

$y'' %2B y = 0~$

the Neumann boundary conditions on the interval $[a, \, b]$ take the form:

$y'(a)= \alpha \ \text{and} \ y'(b) = \beta$

where $\alpha$ and $\beta$ are given numbers.

For a partial differential equation, for instance:

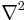$\nabla^2 y %2B y = 0$

where $\nabla^2$ denotes the Laplacian, the Neumann boundary conditions on a domain 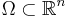$\Omega \subset \mathbb{R}^n$ take the form:

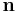$\frac{\partial y}{\partial \mathbf{n}}(x) = f(x) \quad \forall x \in \partial \Omega.$

where $\mathbf{n}$ denotes the (typically exterior) normal to the boundary 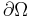$\partial \Omega$ and f is a given scalar function.

The normal derivative which shows up on the left-hand side is defined as:

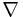$\frac{\partial y}{\partial \mathbf{n}}(x)=\nabla y(x)\cdot \mathbf{n}(x)$

where $\nabla$ is the gradient (vector) and the dot is the inner product.

Many other boundary conditions are possible. For example, there is the Cauchy boundary condition, or the mixed boundary condition which is a combination of the Dirichlet and Neumann conditions.

References

^ Cheng, A. and D. T. Cheng (2005). Heritage and early history of the boundary element method, Engineering Analysis with Boundary Elements, 29, 268–302.

Neumann boundary condition

See also

References