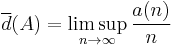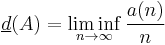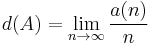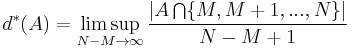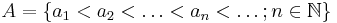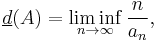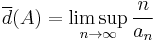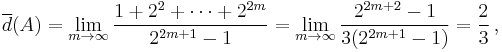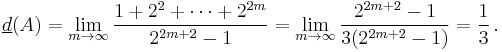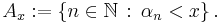Natural density
In number theory, asymptotic density (or natural density or arithmetic density) is one of the possibilities to measure how large a subset of the set of natural numbers is.
Intuitively, it is thought that there are more positive integers than perfect squares, since every perfect square is already positive, and many other positive integers exist besides. However, the set of positive integers is not in fact greater than the set of perfect squares: both sets are infinite and countable and can therefore be put in one-to-one correspondence.
If an integer is randomly selected from the set [1,n], then the probability that it belongs to A is the ratio of the number of elements of A in [1,n] to the total number of elements in [1,n]. If this probability tends to some limit as n tends to infinity, then this limit is referred to as the asymptotic density of A. This notion can be understood as a kind of probability of choosing a number from the set A. Indeed, the asymptotic density (as well as some other types of densities) is studied in probabilistic number theory.
Asymptotic density contrasts, for example, with the Schnirelmann density. A drawback of this approach is that the asymptotic density is not defined for all subsets of 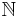 .
.
Contents |
Definition
A subset A of positive integers has natural density (or asymptotic density) α, where
- 0 ≤ α ≤ 1,
if the proportion of elements of A among all natural numbers from 1 to n is asymptotic to α as n tends to infinity.
More explicitly, if one defines for any natural number n the counting function a(n) as the number of elements of A less than or equal to n, then the natural density of A being α exactly means that
- a(n)/n → α as n → +∞.
Upper and lower asymptotic density
Let  be a subset of the set of natural numbers
be a subset of the set of natural numbers 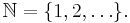 For any
For any 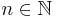 put
put 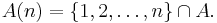 and
and 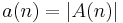 .
.
Define the upper asymptotic density 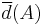 of
of  by
by
where lim sup is the limit superior. 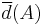 is also known simply as the upper density of
is also known simply as the upper density of 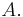
Similarly, 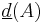 , the lower asymptotic density of
, the lower asymptotic density of  , is defined by
, is defined by
One may say  has asymptotic density
has asymptotic density 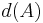 if
if  , in which case it is that
, in which case it is that 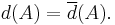
This definition can be restated in the following way:
if the limit exists.
A somewhat weaker notion of density is upper Banach density; given a set 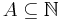 , define
, define 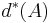 as
as
If one were to write a subset of 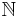 as an increasing sequence
as an increasing sequence
then
and 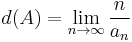 if the limit exists.
if the limit exists.
Examples
- If d(A) exists for some set A, then for the complement set we have d(Ac) = 1 - d(A).
- Obviously, d(N) = 1.
- For any finite set F of positive integers, d(F) = 0.
- If
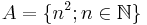 is the set of all squares, then d(A) = 0.
is the set of all squares, then d(A) = 0. - If
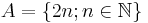 is the set of all even numbers, then d(A) = 1/2. Similarly, for any arithmetical progression
is the set of all even numbers, then d(A) = 1/2. Similarly, for any arithmetical progression 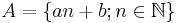 we get d(A) = 1/a.
we get d(A) = 1/a. - For the set P of all primes we get from the prime number theorem d(P) = 0.
- The set of all square-free integers has density
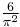
- The density of the set of abundant numbers is known to be between 0.2474 and 0.2480.
- The set
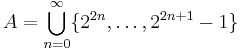 of numbers whose binary expansion contains an odd number of digits is an example of a set which does not have an asymptotic density, since the upper density of this set is
of numbers whose binary expansion contains an odd number of digits is an example of a set which does not have an asymptotic density, since the upper density of this set is
-
- whereas its lower density is
- Consider an equidistributed sequence
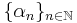 in
in ![[0,1]:](/2012-wikipedia_en_all_nopic_01_2012/I/3a4365e64bdd5d550aad5307979b3b9e.png) and define a monotone family
and define a monotone family ![\{A_x\}_{x\in[0,1]}](/2012-wikipedia_en_all_nopic_01_2012/I/96565b4412a9dfb92bb878b1639c419d.png) of sets :
of sets :
- Then, by definition,
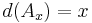 for all
for all  .
.
References
- H. H. Ostmann (1956) (in German). Additive Zahlentheorie I. Berlin-Göttingen-Heidelberg: Springer-Verlag.
- Steuding, Jörn. "Probabilistic number theory". http://www.math.uni-frankfurt.de/~steuding/steuding/prob.pdf. Retrieved 2005-10-06.
- G. Tenenbaum (1995). Introduction to analytic and probabilistic number theory. Cambridge: Cambridge Univ. Press.
This article incorporates material from Asymptotic density on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.