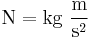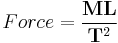Newton (unit)
|
|
|
| Unit system: | SI derived unit |
| Unit of... | Force |
| Symbol: | N |
| Named after: | Isaac Newton |
| In SI base units: | 1 N = 1 kg·m/s2 |
The newton (symbol: N) is the SI derived unit of force. It is named after Isaac Newton in recognition of his work on classical mechanics, specifically Newton's second law of motion.
Contents |
Definition
The newton is the SI unit for force; it is equal to the amount of net force required to accelerate a mass of one kilogram at a rate of one metre per second squared. Newton's second law of motion states: F = ma, multiplying m (kg) by a (m/s2), The newton is therefore:[1]
Units used:
where
- M = Mass
- L = Length
- T = Time
Examples
- 1 N is the force of Earth's gravity on a mass of about 100 g = (1⁄9.81 kg).
- On Earth's surface, a mass of 1 kg exerts a force of approximately 9.8 N [down] (or 1.0 kilogram-force; 1 kgf = 9.80665 N by definition). The approximation of 1 kgf corresponding to 10 N (1 decanewton or daN) is sometimes used as a rule of thumb in everyday life and in engineering.
- The force of Earth's gravity on a human being with a mass of 70 kg is approximately 686 N.
- The dot product of force and distance is mechanical work. Thus, in SI units, a force of 1 N exerted over a distance of 1 m is 1 N·m of work. The Work-Energy Theorem states that the work done on a body is equal to the change in energy of the body. 1 N·m = 1 J (joule), the SI unit of energy.
- It is common to see forces expressed in kilonewtons or kN, where 1 kN = 1,000 N.
Common use of kilonewtons in construction
Kilonewtons are often used for stating safety holding values of fasteners, anchors, and more in the building industry. They are also often used in the specifications for rock climbing equipment. The safe working loads in both tension and shear measurements can be stated in kilonewtons. Injection moulding machines, used to manufacture plastic parts, are classed by kilonewton (i.e., the amount of clamping force they apply to the mould).
On the Earth's surface, 1 kN is about 101.97162 kilogram-force of load, but multiplying the kilonewton value by 100 (i.e. using a slightly conservative and easier to calculate value) is a good rule of thumb.[2]
Conversion factors
| newton (SI unit) |
dyne | kilogram-force, kilopond |
pound-force | poundal | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg·m/s² | = 105 dyn | ≈ 0.10197 kp | ≈ 0.22481 lbF | ≈ 7.2330 pdl |
| 1 dyn | = 10−5 N | ≡ 1 g·cm/s² | ≈ 1.0197×10−6 kp | ≈ 2.2481×10−6 lbF | ≈ 7.2330×10−5 pdl |
| 1 kp | = 9.80665 N | = 980665 dyn | ≡ gn·(1 kg) | ≈ 2.2046 lbF | ≈ 70.932 pdl |
| 1 lbF | ≈ 4.448222 N | ≈ 444822 dyn | ≈ 0.45359 kp | ≡ gn·(1 lb) | ≈ 32.174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 dyn | ≈ 0.014098 kp | ≈ 0.031081 lbF | ≡ 1 lb·ft/s² |
| The value of gn as used in the official definition of the kilogram-force is used here for all gravitational units. | |||||
| Base | force, length, time | weight, length, time | mass, length, time | |||||
|---|---|---|---|---|---|---|---|---|
| Force (F) | 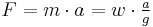 |
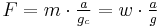 |
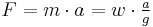 |
|||||
| Weight (w) | 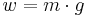 |
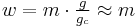 |
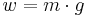 |
|||||
| System | BG | GM | EE | M | AE | CGS | MTS | SI |
| Acceleration (a) | ft/s2 | m/s2 | ft/s2 | m/s2 | ft/s2 | Gal | m/s2 | m/s2 |
| Mass (m) | slug | hyl | lbm | kg | lb | g | t | kg |
| Force (F) | lb | kp | lbF | kp | pdl | dyn | sn | N |
| Pressure (p) | lb/in2 | at | PSI | atm | pdl/ft2 | Ba | pz | Pa |
See also
- Force gauge
- International System of Units (SI)
- Orders of magnitude (force)
- Joule, SI unit of energy, 1 newton exerted over a distance of 1 metre
- Kilogram-force, force exerted by Earth's gravity at sea level on one kilogram of mass
- Pascal, SI unit of pressure, 1 newton acting on an area of 1 square metre
- Isaac Newton#Apple analogy The history of the falling apple
References
- ^ "Table 3. Coherent derived units in the SI with special names and symbols". The International System of Units (SI). International Bureau of Weights and Measures. 2006. http://www.bipm.org/en/si/si_brochure/chapter2/2-2/table3.html.
- ^ http://www.convertunits.com/from/kilonewtons/to/kilograms-force
- ^ Lindeburg, Michael, Civil Engineering Reference Manual for the PE Exam
- ^ Wurbs, Ralph A, Fort Hood Review Sessions for Professional Engineering Exam, http://engineeringregistration.tamu.edu/tapedreviews/Fluids-PE/PDF/Fluids-PE.pdf, retrieved October 26, 2011
|
||||||||||||||||||||