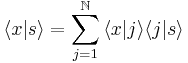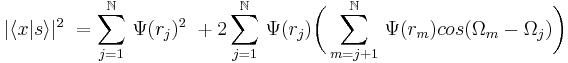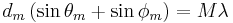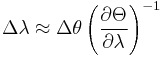N-slit interferometric equation

Quantum mechanics was first applied to optics, and interference in particular, by Paul Dirac.[1] Feynman, in his lectures, uses Dirac’s notation to describe thought experiments on double-slit interference of electrons.[2] Feynman’s approach was extended to N-slit interferometers using narrow-linewidth laser illumination, that is, illumination by indistinguishable photons, by researchers working on the measurement of complex interference patterns.[3]

Contents

Probability amplitudes and the N-slit interferometric equation

In this approach the probability amplitude for propagation from a source (s) to an interference plane (x) via an array of slits (j) is given, using Dirac’s notation, as[3]

\langle x | s \rangle = \sum_{j=1}^\N\, \langle x | j \rangle \langle j | s \rangle

Using a wavefunction representation for probability amplitudes,[1] after some algebra, the corresponding probability becomes[3][4][5]

|\langle x | s \rangle|^2\ = \sum_{j=1}^\N\,\Psi(r_j)^2\ %2B2 \sum_{j=1}^\N\,\Psi(r_j)\bigg(\sum_{m=j%2B1}^\N\,\Psi(r_m)cos(\Omega_m-\Omega_j)\bigg)

where N is the total number of slits in the array, or transmission grating, and the term in parenthesis represents the phase that is directly related to the exact geometry of the N-slit interferometer. The Dirac-Duarte interferometric equation applies to the propagation of a single photon, or the propagation of an ensemble of indistinguishable photons, and enables the accurate prediction of measured N-slit interferometric patterns continuously from the near to the far field.[5][6] Interferograms generated with this equation have been shown to compare well with measured interferograms for both even (N = 2, 4, 6...) and odd (N = 3, 5, 7...) values of N from 2 to 1600.[5][7]

Applications

At a practical level, the N-slit interferometric equation was introduced for imaging applications[5] and is routinely applied to predict N-slit laser interferograms, both in the near and far field. Thus, it has become a valuable tool in the alignment of large, and very large, N-slit laser interferometers[8][9] used in the study of clear air turbulence and the propagation of interferometric characters for secure free-space optical communications.

Also, the N-slit interferometric equation has been applied to describe interference, diffraction, refraction (Snell's law), and reflection, in a rational and unified approach, using quantum mechanics principles.[7][10][11] For example, the phase term (in parenthesis) can be used to derive[7][10]

d_m \left( \sin{\theta_m} %2B \sin{\phi_m} \right) = M \lambda

which is also known as the diffraction grating equation. Here, 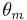\theta_m is the angle of incidence, 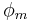\phi_m is the angle of diffraction, \lambda is the wavelength, and M is the order of diffraction.

Further, the N-slit interferometric equation has been applied to derive the cavity linewidth equation applicable to dispersive oscillators, such as the multiple-prism grating laser oscillators:[12]

\Delta\lambda \approx \Delta \theta \left({\partial\Theta\over\partial\lambda}\right)^{-1}

In this equation, 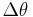\Delta \theta is the beam divergence and the overall intracavity angular dispersion is the quantity in parenthesis (elevated to –1).

The N-slit interferometric approach[5][7][10] is one of several approaches applied to describe basic optical phenomena in a cohesive and unified manner.[13]

Note: given the various terminologies in use, for N-slit interferometry, it should be made explicit that the N-slit interferometric equation applies to two-slit interference, three-slit interference, four-slit interference, etc.

See also

References

  1. ^ a b P. A. M. Dirac, The Principles of Quantum Mechanics, 4th Ed. (Oxford, London, 1978).
  2. ^ R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol. III (Addison Wesley, Reading, 1965).
  3. ^ a b c F. J. Duarte and D. J. Paine, Quantum mechanical description of N-slit interference phenomena, in Proceedings of the International Conference on Lasers '88, R. C. Sze and F. J. Duarte (Eds.) (STS, McLean, Va, 1989) pp. 42-47.
  4. ^ F. J. Duarte, Dispersive dye lasers, in High Power Dye Lasers, F. J. Duarte (Ed.) (Springer-Verlag, Berlin, 1991) Chapter 2.
  5. ^ a b c d e F. J. Duarte, On a generalized interference equation and interferometric measurements, Opt. Commun. 103, 8-14 (1993).
  6. ^ F. J. Duarte, Comment on "reflection, refraction, and multislit interfernce," Eur. J. Phys. 25, L57-L58 (2004).
  7. ^ a b c d F. J. Duarte, Tunable Laser Optics (Elsevier-Academic, New York, 2003).
  8. ^ F. J. Duarte, T. S. Taylor, A. B. Clark, and W. E. Davenport, The N-slit interferometer: an extended configuration, J. Opt. 12, 015705 (2010).
  9. ^ a b F. J. Duarte, T. S. Taylor, A. M. Black, W. E. Davenport, and P. G. Varmette, N-slit interferometer for secure free-space optical communications: 527 m intra interferometric path length , J. Opt. 13, 035710 (2011).
  10. ^ a b c F. J. Duarte, Interference, diffraction, and refraction, via Dirac's notation, Am. J. Phys. 65, 637-640 (1997).
  11. ^ F. J. Duarte, Multiple-prism dispersion equations for positive and negative refraction, Appl. Phys. B 82, 35-38 (2006).
  12. ^ F. J. Duarte, Cavity dispersion equation: a note on its origin, Appl. Opt. 31, 6979-6982 (1992).
  13. ^ J. Kurusingal, Law of normal scattering - a comprehensive law for wave propagation at an interface, J. Opt. Soc. Am. A 24, 98-108 (2007).

External links