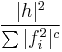Multiplier ideal

In commutative algebra, the multiplier ideal associated to a sheaf of ideals over a complex variety and a real number c consists (locally) of the functions h such that

$\frac{|h|^2}{\sum|f_i^2|^c}$

is locally integrable, where the f_i are a finite set of local generators of the ideal. Multiplier ideals were independently introduced by Nadel (1989) (who worked with sheaves over complex manifolds rather than ideals) and Lipman (1993), who called them adjoint ideals.

Multiplier ideals are discussed in the survey articles Blickle & Lazarsfeld (2004), Siu (2005), and Lazarsfeld (2009).

References

Blickle, Manuel; Lazarsfeld, Robert (2004), "An informal introduction to multiplier ideals", Trends in commutative algebra, Math. Sci. Res. Inst. Publ., 51, Cambridge University Press, pp. 87–114, MR 2132649, http://www.msri.org/communications/books/Book51/contents.html
Lazarsfeld, Robert (2009), "A short course on multiplier ideals", 2008 PCMI lectures, arXiv:0901.0651
Lipman, Joseph (1993), "Adjoints and polars of simple complete ideals in two-dimensional regular local rings", Bulletin de la Société Mathématique de Belgique. Série A 45 (1): 223–244, MR 1316244, http://www.math.purdue.edu/~lipman/papers/polars.pdf
Nadel, Alan Michael (1989), "Multiplier ideal sheaves and existence of Kähler-Einstein metrics of positive scalar curvature", Proceedings of the National Academy of Sciences of the United States of America 86 (19): 7299–7300, JSTOR 34630, MR 1015491
Siu, Yum-Tong (2005), "Multiplier ideal sheaves in complex and algebraic geometry", Science in China. Series A. Mathematics 48: 1–31, doi:10.1007/BF02884693, MR 2156488