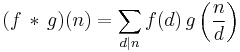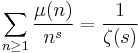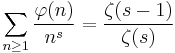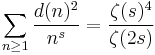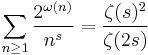Multiplicative function
- Outside number theory, the term multiplicative function is usually used for completely multiplicative functions. This article discusses number theoretic multiplicative functions.
In number theory, a multiplicative function is an arithmetic function f(n) of the positive integer n with the property that f(1) = 1 and whenever a and b are coprime, then
- f(ab) = f(a) f(b).
An arithmetic function f(n) is said to be completely multiplicative (or totally multiplicative) if f(1) = 1 and f(ab) = f(a) f(b) holds for all positive integers a and b, even when they are not coprime.
Contents |
Examples
Some multiplicative functions are defined to make formulas easier to write:
- 1(n): the constant function, defined by 1(n) = 1 (completely multiplicative)
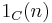 the indicator function of the set
the indicator function of the set 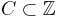 . This is multiplicative if the set C has the property that if a and b are in C, gcd(a, b)=1, than ab is also in C. This is the case if C is the set of squares, cubes, or higher powers, or if C is the set of square-free numbers.
. This is multiplicative if the set C has the property that if a and b are in C, gcd(a, b)=1, than ab is also in C. This is the case if C is the set of squares, cubes, or higher powers, or if C is the set of square-free numbers.
- Id(n): identity function, defined by Id(n) = n (completely multiplicative)
- Idk(n): the power functions, defined by Idk(n) = nk for any complex number k (completely multiplicative). As special cases we have
- Id0(n) = 1(n) and
- Id1(n) = Id(n).
 (n): the function defined by
(n): the function defined by  (n) = 1 if n = 1 and 0 otherwise, sometimes called multiplication unit for Dirichlet convolution or simply the unit function; the Kronecker delta δin; sometimes written as u(n), not to be confused with
(n) = 1 if n = 1 and 0 otherwise, sometimes called multiplication unit for Dirichlet convolution or simply the unit function; the Kronecker delta δin; sometimes written as u(n), not to be confused with  (n) (completely multiplicative).
(n) (completely multiplicative).
Other examples of multiplicative functions include many functions of importance in number theory, such as:
- gcd(n,k): the greatest common divisor of n and k, as a function of n, where k is a fixed integer.
 (n): Euler's totient function
(n): Euler's totient function  , counting the positive integers coprime to (but not bigger than) n
, counting the positive integers coprime to (but not bigger than) n
 (n): the Möbius function, the parity (−1 for odd, +1 for even) of the number of prime factors of square-free numbers; 0 if n is not square-free
(n): the Möbius function, the parity (−1 for odd, +1 for even) of the number of prime factors of square-free numbers; 0 if n is not square-free
 k(n): the divisor function, which is the sum of the k-th powers of all the positive divisors of n (where k may be any complex number). Special cases we have
k(n): the divisor function, which is the sum of the k-th powers of all the positive divisors of n (where k may be any complex number). Special cases we have
 0(n) = d(n) the number of positive divisors of n,
0(n) = d(n) the number of positive divisors of n, 1(n) =
1(n) =  (n), the sum of all the positive divisors of n.
(n), the sum of all the positive divisors of n.
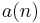 : the number of non-isomorphic abelian groups of order n.
: the number of non-isomorphic abelian groups of order n.
 (n): the Liouville function, λ(n) = (−1)Ω(n) where Ω(n) is the total number of primes (counted with multiplicity) dividig n. (completely multiplicative).
(n): the Liouville function, λ(n) = (−1)Ω(n) where Ω(n) is the total number of primes (counted with multiplicity) dividig n. (completely multiplicative).
 (n), defined by
(n), defined by  (n) = (−1)
(n) = (−1) (n), where the additive function
(n), where the additive function  (n) is the number of distinct primes dividing n.
(n) is the number of distinct primes dividing n.
- All Dirichlet characters are completely multiplicative functions. For example
- (n/p), the Legendre symbol, considered as a function of n where p is a fixed prime number.
An example of a non-multiplicative function is the arithmetic function r2(n) - the number of representations of n as a sum of squares of two integers, positive, negative, or zero, where in counting the number of ways, reversal of order is allowed. For example:
- 1 = 12 + 02 = (-1)2 + 02 = 02 + 12 = 02 + (-1)2
and therefore r2(1) = 4 ≠ 1. This shows that the function is not multiplicative. However, r2(n)/4 is multiplicative.
In the On-Line Encyclopedia of Integer Sequences, sequences of values of a multiplicative function have the keyword "mult".
See arithmetic function for some other examples of non-multiplicative functions.
Properties
A multiplicative function is completely determined by its values at the powers of prime numbers, a consequence of the fundamental theorem of arithmetic. Thus, if n is a product of powers of distinct primes, say n = pa qb ..., then f(n) = f(pa) f(qb) ...
This property of multiplicative functions significantly reduces the need for computation, as in the following examples for n = 144 = 24 · 32:
- d(144) =
 0(144) =
0(144) =  0(24)
0(24) 0(32) = (10 + 20 + 40 + 80 + 160)(10 + 30 + 90) = 5 · 3 = 15,
0(32) = (10 + 20 + 40 + 80 + 160)(10 + 30 + 90) = 5 · 3 = 15,  (144) =
(144) =  1(144) =
1(144) =  1(24)
1(24) 1(32) = (11 + 21 + 41 + 81 + 161)(11 + 31 + 91) = 31 · 13 = 403,
1(32) = (11 + 21 + 41 + 81 + 161)(11 + 31 + 91) = 31 · 13 = 403, *(144) =
*(144) =  *(24)
*(24) *(32) = (11 + 161)(11 + 91) = 17 · 10 = 170.
*(32) = (11 + 161)(11 + 91) = 17 · 10 = 170.
Similarly, we have:
 (144)=
(144)= (24)
(24) (32) = 8 · 6 = 48
(32) = 8 · 6 = 48
In general, if f(n) is a multiplicative function and a, b are any two positive integers, then
Every completely multiplicative function is a homomorphism of monoids and is completely determined by its restriction to the prime numbers.
Convolution
If f and g are two multiplicative functions, one defines a new multiplicative function f * g, the Dirichlet convolution of f and g, by
where the sum extends over all positive divisors d of n. With this operation, the set of all multiplicative functions turns into an abelian group; the identity element is  .
.
Relations among the multiplicative functions discussed above include:
 * 1 =
* 1 =  (the Möbius inversion formula)
(the Möbius inversion formula)- (
 * Idk) * Idk =
* Idk) * Idk =  (generalized Möbius inversion)
(generalized Möbius inversion)  * 1 = Id
* 1 = Id- d = 1 * 1
 = Id * 1 =
= Id * 1 =  * d
* d k = Idk * 1
k = Idk * 1- Id =
 * 1 =
* 1 =  *
* 
- Idk =
 k *
k * 
The Dirichlet convolution can be defined for general arithmetic functions, and yields a ring structure, the Dirichlet ring.
Dirichlet series for some multiplicative functions
More examples are shown in the article on Dirichlet series.
See also
References
- See chapter 2 of Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR0434929