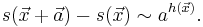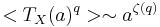Multifractal system
A multifractal system is a generalization of a fractal system in which a single exponent (the fractal dimension) is not enough to describe its dynamics; instead, a continuous spectrum of exponents (the so-called singularity spectrum) is needed.
Multifractal systems are common in nature, especially geophysics. They include fully developed turbulence, stock market time series, real world scenes, the Sun’s magnetic field time series, heartbeat dynamics, human gait, and natural luminosity time series. Models have been proposed in various contexts ranging from turbulence in fluid dynamics to internet traffic, finance, image modeling, texture synthesis, meteorology, geophysics and more.
In a multifractal system  , the behavior around any point is described by a local power law:
, the behavior around any point is described by a local power law:
The exponent 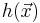 is called the singularity exponent, as it describes the local degree of singularity or regularity around the point
is called the singularity exponent, as it describes the local degree of singularity or regularity around the point 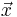 .
.
The ensemble formed by all the points that share the same singularity exponent is called the singularity manifold of exponent h, and is a fractal set of fractal dimension D(h). The curve D(h) versus h is called the singularity spectrum and fully describes the (statistical) distribution of the variable  .
.
In practice, the multifractal behaviour of a physical system  is not directly characterized by its singularity specrum D(h). Data analysis rather gives access to the multiscaling exponents
is not directly characterized by its singularity specrum D(h). Data analysis rather gives access to the multiscaling exponents 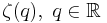 . Indeed, multifractal signals generally obey a scale invariance property which yields power law behaviours for multiresolution quantities depending on their scale
. Indeed, multifractal signals generally obey a scale invariance property which yields power law behaviours for multiresolution quantities depending on their scale  . Depending on the object under study, these multiresolution quantities, denoted by
. Depending on the object under study, these multiresolution quantities, denoted by 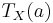 in the following, can be local averages in boxes of size
in the following, can be local averages in boxes of size  , gradients over distance
, gradients over distance  , wavelet coefficients at scale
, wavelet coefficients at scale  ... For multifractal objects, one usually observes a global power law scaling of the form:
... For multifractal objects, one usually observes a global power law scaling of the form:
at least in some range of scales and for some range of orders  . When such a behaviour is observed, one talks of scale invariance, self-similarity or multiscaling.
. When such a behaviour is observed, one talks of scale invariance, self-similarity or multiscaling.
Contents |
Estimation
Thanks to the so-called multifractal formalism, it can be shown that, under some well-suited assumptions, there exists a correspondence between the singularity spectrum 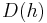 and the multiscaling exponents
and the multiscaling exponents 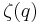 through a Legendre transform. While the determination of
through a Legendre transform. While the determination of 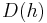 calls for some exhaustive local analysis of the data, which would result difficult and numerically unstable, the estimation of the
calls for some exhaustive local analysis of the data, which would result difficult and numerically unstable, the estimation of the 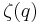 relies on the use of statistical averages and linear regressions in log-log diagrams. Once the
relies on the use of statistical averages and linear regressions in log-log diagrams. Once the 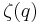 are known, one can deduce an estimate of
are known, one can deduce an estimate of 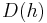 thanks to a simple Legendre transform.
thanks to a simple Legendre transform.
Multifractal systems are often modeled by stochastic processes such as multiplicative cascades. Interestingly, the 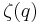 receives some statistical interpretation as they characterize the evolution of the distributions of the
receives some statistical interpretation as they characterize the evolution of the distributions of the 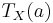 as
as  goes from larger to smaller scales. This evolution is often called statistical intermittency and betrays a departure from Gaussian models.
goes from larger to smaller scales. This evolution is often called statistical intermittency and betrays a departure from Gaussian models.
Modelling as a multiplicative cascade also leads to estimation of multifractal properties for relatively small datasets (Roberts & Cronin 1996). A maximum likelihood fit of a multiplicative cascade to the dataset not only estimates the complete spectrum, but also gives reasonable estimates of the errors (see the web service [1]).
See also
- Multifractal Model of Asset Returns (MMAR)
- Multifractal Random Walk model (MRW)
- Fractional Brownian motion
- Mandelbrot cascade, continuous cascade and lognormal cascade
References
- A.J. Roberts and A. Cronin (1996). "Unbiased estimation of multi-fractal dimensions of finite data sets". Physica A 233: 867–878. doi:10.1016/S0378-4371(96)00165-3.
External links
- Stanley H.E., Meakin P. (1988). "Multifractal phenomena in physics and chemistry" (Review). Nature 335 (6189): 405–9. doi:10.1038/335405a0. http://polymer.bu.edu/hes/articles/sm88.pdf.
- Alain Arneodo, et al. (2008). "Wavelet-based multifractal analysis". Scholarpedia 3 (3): 4103. doi:10.4249/scholarpedia.4103. http://www.scholarpedia.org/article/Wavelet-based_multifractal_analysis.