Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, (also called "parallel edges"[1]), that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge.
There are two distinct notions of multiple edges. One says that, as in graphs without multiple edges, the identity of an edge is defined by the nodes it connects, but the same edge can occur several times between these nodes. Alternatively, one defines edges to be first-class entities like nodes, each having its own identity independent of the nodes it connects.
Contents |
Undirected multigraph (edges without own identity)
Formally, a multigraph G is an ordered pair G:=(V, E) with
Multigraphs might be used to model the possible flight connections offered by an airline. In this case the multigraph would be a directed graph with pairs of directed parallel edges connecting cities to show that it is possible to fly both to and from these locations.
Some authors also allow multigraphs to have loops, that is, an edge that connects a vertex to itself,[2] while others call these pseudographs, reserving the term multigraph for the case with no loops.[3]
Directed multigraph (edges without own identity)
A multidigraph is a directed graph which is permitted to have multiple arcs, i.e., arcs with the same source and target nodes. A multidigraph G is an ordered pair G:=(V,A) with
- V a set of vertices or nodes,
- A a multiset of ordered pairs of vertices called directed edges, arcs or arrows.
A mixed multigraph G:=(V,E, A) may be defined in the same way as a mixed graph.
Directed multigraph (edges with own identity)
A multidigraph G is an ordered 4-tuple G:=(V, A, s, t) with
- V a set of vertices or nodes,
- A a set of edges or lines,
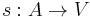 , assigning to each edge its source node,
, assigning to each edge its source node,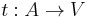 , assigning to each edge its target node.
, assigning to each edge its target node.
In category theory a small category can be defined as a multidigraph (with edges having their own identity) equipped with an associative composition law and a distinguished self-loop at each vertex serving as the left and right identity for composition. For this reason, in category theory the term graph is standardly taken to mean "multidigraph", and the underlying multidigraph of a category is called its underlying digraph.
Labeling
Multigraphs and multidigraphs also support the notion of graph labeling, in a similar way. However there is no unity in terminology in this case.
The definitions of labeled multigraphs and labeled multidigraphs are similar, and we define only the latter ones here.
Definition 1: A labeled multidigraph is a labeled graph with labeled arcs.
Formally: A labeled multidigraph G is a multigraph with labeled vertices and arcs. Formally it is an 8-tuple 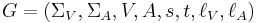 where
where
- V is a set of vertices and A is a set of arcs.
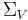 and
and 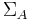 are finite alphabets of the available vertex and arc labels,
are finite alphabets of the available vertex and arc labels, and
and 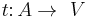 are two maps indicating the source and target vertex of an arc,
are two maps indicating the source and target vertex of an arc,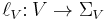 and
and 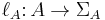 are two maps describing the labeling of the vertices and arcs.
are two maps describing the labeling of the vertices and arcs.
Definition 2: A labeled multidigraph is a labeled graph with multiple labeled arcs, i.e. arcs with the same end vertices and the same arc label (note that this notion of a labeled graph is different from the notion given by the article graph labeling).
Notes
References
- Balakrishnan, V. K.; Graph Theory, McGraw-Hill; 1 edition (February 1, 1997). ISBN 0-07-005489-4.
- Bollobas, Bela; Modern Graph Theory, Springer; 1st edition (August 12, 2002). ISBN 0-387-98488-7.
- Diestel, Reinhard; Graph Theory, Springer; 2nd edition (February 18, 2000). ISBN 0-387-98976-5.
- Gross, Jonathan L, and Yellen, Jay; Graph Theory and Its Applications, CRC Press (December 30, 1998). ISBN 0-8493-3982-0.
- Gross, Jonathan L, and Yellen, Jay; (eds); Handbook of Graph Theory. CRC (December 29, 2003). ISBN 1-58488-090-2.
- Harary, Frank; Graph Theory, Addison Wesley Publishing Company (January 1995). ISBN 0-201-41033-8.
- Zwillinger, Daniel; CRC Standard Mathematical Tables and Formulae, Chapman & Hall/CRC; 31st edition (November 27, 2002). ISBN 1-58488-291-3.
- Janson, Svante; Knuth, Donald E.; Luczak, Tomasz; Pittel, Boris (1993). "The birth of the giant component". Random Structures and Algorithms 4 (3): 231–358. doi:10.1002/rsa.3240040303. ISBN 3240040303. MR1220220.
External links
- Paul E. Black, Multigraph at the NIST Dictionary of Algorithms and Data Structures.