Muller automaton

In automata theory, a Muller automaton is a type of an ω-automaton. The acceptance condition separates a Muller automomaton from other ω-automata. The Muller automata is defined using Muller acceptance condition, i.e. the set of all states visited infinitely often must be an element of the acceptance set. Both deterministic and non-deterministic Muller automata recognize the ω-regular languages.

1 Formal definition
2 Equivalence with other ω-automata
3 Transformation to non-deterministic muller automaton
4 Transformation to deterministic muller automaton
5 References

Formal definition

Formally, a deterministic Muller-automaton is a tuple A = (Q,Σ,δ,q₀,F) that consists of the following information:

Q is a finite set. The elements of Q are called the states of Q.
Σ is a finite set called the alphabet of A.
δ: Q × Σ → Q is a function, called the transition function of A.
q₀ is an element of Q, called the initial state.
F is set of sets of states. Formally, F ⊆ P(Q) where P(Q) is powerset of Q. F defines the acceptance condition.A accepts exactly those runs in which the set of infinitely often occurring states is an element of F

In a non-deterministic Muller automaton, the transition function δ is replaced with a transition relation Δ that returns a set of states and initial state is q₀ is replaced by a set of initial states Q₀. Generally, Muller automaton refers to non-deterministic Muller automaton.

For more comprehensive formalism look at ω-automaton.

Equivalence with other ω-automata

The Muller automata are equally expressive as parity automata, Rabin Automata, Streett automata, and non-deterministic Büchi automata, to mention some, and strictly more expressive than the deterministic Büchi automata. The equivalence of the above automata and non-deterministic Muller automata can be shown very easily as the accepting conditions of these automata can be emulated using the acceptance condition of Muller automata. McNaughton's Theorem demonstrates the equivalence of non-deterministic Büchi automaton and deterministic Muller automaton. Thus, deterministic and non-deterministic Muller automaton are equivalent in terms of the languages they can accept.

Transformation to non-deterministic muller automaton

Following is a list of automata constructions which transforms a type of ω-automata to a non-deterministic muller automaton.

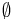From Büchi automaton: If $B$ is the set of final states in a Büchi automata with the set of states $Q$ , we can construct a Muller automata with same set of states, transition function and initial state with the muller accepting condition as F = { X | X ∈ 2^Q ∧ X ∩ B ≠ $\emptyset$ }

From Rabin automaton/Parity automaton: Similarly, the Rabin conditions 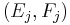$(E_j,F_j)$ can be emulated by constructing the acceptance set in the Muller automata as all sets in 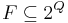$F \subseteq 2^Q$ which satisfy 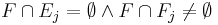$F \cap E_j = \emptyset \and F \cap F_j \neq \emptyset$ , for some j. Note that this covers the case of Parity automaton too, as the Parity acceptance condition can be expressed as Rabin acceptance condition easily.

From Streett automaton: The Streett conditions 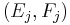$(E_j,F_j)$ can be emulated by constructing the acceptance set in the Muller automata as all sets in 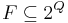$F \subseteq 2^Q$ which satisfy 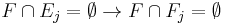$F \cap E_j = \emptyset \rightarrow F \cap F_j = \emptyset$ , for all j.

Transformation to deterministic muller automaton

Union of two deterministic muller automaton

From Büchi automaton

McNaughton's Theorem provides a procedure to transform non-deterministic Büchi automaton to deterministic Muller automaton.

References

Automata on Infinite Words Slides for a tutorial by Paritosh K. Pandya.
Yde Venema (2008) Lectures on the Modal μ-calculus; the 2006 version was presented at The 18th European Summer School in Logic, Language and Information