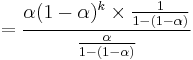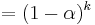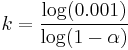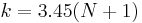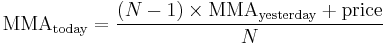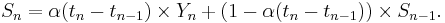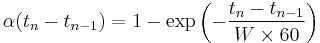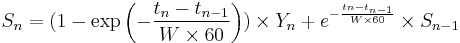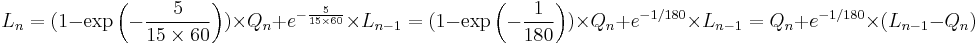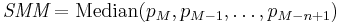Moving average
In statistics, a moving average, also called rolling average, rolling mean or running average, is a type of finite impulse response filter used to analyze a set of data points by creating a series of averages of different subsets of the full data set.
Given a series of numbers and a fixed subset size, the moving average can be obtained by first taking the average of the first subset. The fixed subset size is then shifted forward, creating a new subset of numbers, which is averaged. This process is repeated over the entire data series. The plot line connecting all the (fixed) averages is the moving average. A moving average is a set of numbers, each of which is the average of the corresponding subset of a larger set of data points. A moving average may also use unequal weights for each data value in the subset to emphasize particular values in the subset.
A moving average is commonly used with time series data to smooth out short-term fluctuations and highlight longer-term trends or cycles. The threshold between short-term and long-term depends on the application, and the parameters of the moving average will be set accordingly. For example, it is often used in technical analysis of financial data, like stock prices, returns or trading volumes. It is also used in economics to examine gross domestic product, employment or other macroeconomic time series. Mathematically, a moving average is a type of convolution and so it can be viewed as an example of a low-pass filter used in signal processing. When used with non-time series data, a moving average filters higher frequency components without any specific connection to time, although typically some kind of ordering is implied. Viewed simplistically it can be regarded as smoothing the data.
Contents |
Simple moving average
In financial applications a simple moving average (SMA) is the unweighted mean of the previous n data points. However, in science and engineering the mean is normally taken from an equal number of data either side of a central value. This ensures that variations in the mean are aligned with the variations in the data rather than being shifted in time. An example of a simple unweighted running mean for a 10-day sample of closing price is the mean of the previous 10 days' closing prices. If those prices are 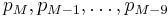 then the formula is
then the formula is
When calculating successive values, a new value comes into the sum and an old value drops out, meaning a full summation each time is unnecessary for this simple case,
The period selected depends on the type of movement of interest, such as short, intermediate, or long term. In financial terms moving average levels can be interpreted as resistance in a rising market, or support in a falling market.
If the data used is not centred around the mean, a simple moving average lags behind the latest data point by half the sample width. A SMA can also be disproportionately influenced by old data points dropping out or new data coming in. One characteristic of the SMA is that if the data have a periodic fluctuation, then applying an SMA of that period will eliminate that variation (the average always containing one complete cycle). But a perfectly regular cycle is rarely encountered.[1]
For a number of applications it is advantageous to avoid the shifting induced by using only 'past' data. Hence a central moving average can be computed, using data equally spaced either side of the point in the series where the mean is calculated. This requires using an odd number of data points in the sample window.
Cumulative moving average
In a cumulative moving average, the data arrives in an ordered data stream and the statistician would like to get the average of all of the data up until the current data point. For example, an investor may want the average price of all of the stock transactions for a particular stock up until the current time. As each new transaction occurs, the average price at the time of the transaction can be calculated for all of the transactions up to that point using the cumulative average, typically an unweighted average of the sequence of i values x1, ..., xi up to the current time:
The brute-force method to calculate this would be to store all of the data and calculate the sum and divide by the number of data points every time a new data point arrived. However, it is possible to simply update cumulative average as a new value xi+1 becomes available, using the formula:
where 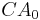 can be taken to be equal to 0.
can be taken to be equal to 0.
Thus the current cumulative average for a new data point is equal to the previous cumulative average plus the difference between the latest data point and the previous average divided by the number of points received so far. When all of the data points arrive (i = N), the cumulative average will equal the final average.
The derivation of the cumulative average formula is straightforward. Using
and similarly for i + 1, it is seen that
Solving this equation for CAi+1 results in:
Weighted moving average
A weighted average is any average that has multiplying factors to give different weights to data at different positions in the sample window. Mathematically, the moving average is the convolution of the data points with a fixed weighting function. One application is removing pixelisation from a digital graphical image.
In technical analysis of financial data, a weighted moving average (WMA) has the specific meaning of weights that decrease in arithmetical progression.[2] In an n-day WMA the latest day has weight n, the second latest n − 1, etc., down to one.
The denominator is a triangle number equal 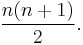 In the more general case the denominator will always be the sum of the individual weights.
In the more general case the denominator will always be the sum of the individual weights.
When calculating the WMA across successive values, the difference between the numerators of WMAM+1 and WMAM is npM+1 − pM − ... − pM−n+1. If we denote the sum pM + ... + pM−n+1 by TotalM, then
The graph at the right shows how the weights decrease, from highest weight for the most recent data points, down to zero. It can be compared to the weights in the exponential moving average which follows.
Exponential moving average
An exponential moving average (EMA), also known as an exponentially weighted moving average (EWMA),[3] is a type of infinite impulse response filter that applies weighting factors which decrease exponentially. The weighting for each older data point decreases exponentially, never reaching zero. The graph at right shows an example of the weight decrease.
The EMA for a series Y may be calculated recursively:
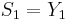
- for
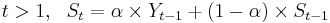
Where:
- The coefficient α represents the degree of weighting decrease, a constant smoothing factor between 0 and 1. A higher α discounts older observations faster. Alternatively, α may be expressed in terms of N time periods, where α = 2/(N+1). For example, N = 19 is equivalent to α = 0.1. The half-life of the weights (the interval over which the weights decrease by a factor of two) is approximately N/2.8854 (within 1% if N > 5).
- Yt is the observation at a time period t.
- St is the value of the EMA at any time period t.
S1 is undefined. S1 may be initialized in a number of different ways, most commonly by setting S1 to Y1, though other techniques exist, such as setting S1 to an average of the first 4 or 5 observations. The prominence of the S1 initialization's effect on the resultant moving average depends on α; smaller α values make the choice of S1 relatively more important than larger α values, since a higher α discounts older observations faster.
This formulation is according to Hunter (1986).[4] By repeated application of this formula for different times, we can eventually write St as a weighted sum of the data points Yt, as:
for any suitable k = 0, 1, 2, ... The weight of the general data point 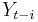 is
is 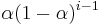 .
.
An alternate approach by Roberts (1959) uses Yt in lieu of Yt−1[5]:
This formula can also be expressed in technical analysis terms as follows, showing how the EMA steps towards the latest data point, but only by a proportion of the difference (each time):
Expanding out 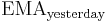 each time results in the following power series, showing how the weighting factor on each data point p1, p2, etc., decreases exponentially:
each time results in the following power series, showing how the weighting factor on each data point p1, p2, etc., decreases exponentially:
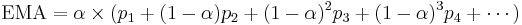
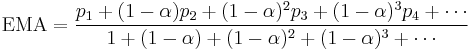 ,
,
since 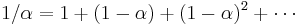 .
.
This is an infinite sum with decreasing terms.
The N periods in an N-day EMA only specify the α factor. N is not a stopping point for the calculation in the way it is in an SMA or WMA. For sufficiently large N, The first N data points in an EMA represent about 86% of the total weight in the calculation[6]:
- i.e.
![\lim_{N \to \infty} \left[1-{\left(1-{2 \over N%2B1}\right)}^{N%2B1} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/cdac07382eae3818db8b424de8a79f33.png) simplified,[7] tends to
simplified,[7] tends to 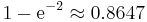 .
.
The power formula above gives a starting value for a particular day, after which the successive days formula shown first can be applied. The question of how far back to go for an initial value depends, in the worst case, on the data. Large price values in old data will affect on the total even if their weighting is very small. If prices have small variations then just the weighting can be considered. The weight omitted by stopping after k terms is
which is
i.e. a fraction
out of the total weight.
For example, to have 99.9% of the weight, set above ratio equal to 0.1% and solve for k:
terms should be used. Since 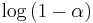 approaches
approaches 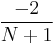 as N increases,[8] this simplifies to approximately[9]
as N increases,[8] this simplifies to approximately[9]
for this example (99.9% weight).
Modified moving average
A modified moving average (MMA), running moving average (RMA), or smoothed moving average is defined as:
In short, this is exponential moving average, with 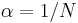 .
.
Application to measuring computer performance
Some computer performance metrics, e.g. the average process queue length, or the average CPU utilization, use a form of exponential moving average.
Here  is defined as a function of time between two readings. An example of a coefficient giving bigger weight to the current reading, and smaller weight to the older readings is
is defined as a function of time between two readings. An example of a coefficient giving bigger weight to the current reading, and smaller weight to the older readings is
where time for readings tn is expressed in seconds, and  is the period of time in minutes over which the reading is said to be averaged (the mean lifetime of each reading in the average). Given the above definition of
is the period of time in minutes over which the reading is said to be averaged (the mean lifetime of each reading in the average). Given the above definition of  , the moving average can be expressed as
, the moving average can be expressed as
For example, a 15-minute average L of a process queue length Q, measured every 5 seconds (time difference is 5 seconds), is computed as
Other weightings
Other weighting systems are used occasionally – for example, in share trading a volume weighting will weight each time period in proportion to its trading volume.
A further weighting, used by actuaries, is Spencer's 15-Point Moving Average[10] (a central moving average). The symmetric weight coefficients are -3, -6, -5, 3, 21, 46, 67, 74, 67, 46, 21, 3, -5, -6, -3.
Outside the world of finance, weighted running means have many forms and applications. Each weighting function or "kernel" has its own characteristics. In engineering and science the frequency and phase response of the filter is often of primary importance in understanding the desired and undesired distortions that a particular filter will apply to the data.
A mean does not just "smooth" the data. A mean is a form of low-pass filter. The effects of the particular filter used should be understood in order to make an appropriate choice.
Moving median
From a statistical point of view, the moving average, when used to estimate the underlying trend in a time series, is susceptible to rare events such as rapid shocks or other anomalies. A more robust estimate of the trend is the simple moving median over n time points:
where the median is found by, for example, sorting the values inside the brackets and finding the value in the middle.
Statistically, the moving average is optimal for recovering the underlying trend of the time series when the fluctuations about the trend are normally distributed. However, the normal distribution does not place high probability on very large deviations from the trend which explains why such deviations will have a disproportionately large effect on the trend estimate. It can be shown that if the fluctuations are instead assumed to be Laplace distributed, then the moving median is statistically optimal.[11] For a given variance, the Laplace distribution places higher probability on rare events than does the normal, which explains why the moving median tolerates shocks better than the moving mean.
When the simple moving median above is central, the smoothing is identical to the median filter which has applications in, for example, image signal processing.
See also
Notes and references
- ^ Statistical Analysis, Ya-lun Chou, Holt International, 1975, ISBN 0030894220, section 17.9.
- ^ "Weighted Moving Averages: The Basics". Investopedia. http://www.investopedia.com/articles/technical/060401.asp.
- ^ http://lorien.ncl.ac.uk/ming/filter/filewma.htm
- ^ NIST/SEMATECH e-Handbook of Statistical Methods: Single Exponential Smoothing at the National Institute of Standards and Technology
- ^ NIST/SEMATECH e-Handbook of Statistical Methods: EWMA Control Charts at the National Institute of Standards and Technology
- ^ The denominator on the left-hand side should be unity, and the numerator will become the right-hand side (geometric series),
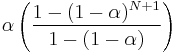 .
. - ^ Because (1+x/n)n becomes ex for large n.
- ^ It means
 -> 0, and the Taylor series of
-> 0, and the Taylor series of 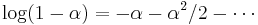 tends to
tends to  .
. - ^ loge(0.001) / 2 = -3.45
- ^ Spencer's 15-Point Moving Average — from Wolfram MathWorld
- ^ G.R. Arce, "Nonlinear Signal Processing: A Statistical Approach", Wiley:New Jersey, USA, 2005.
External links
- EWMA in determining network traffic and ethernet
- FastMedFilt1D: Fast Matlab software for computing the simple moving median of a time series.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
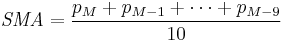
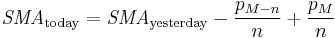
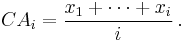
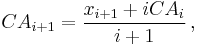
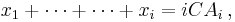
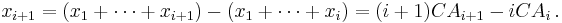
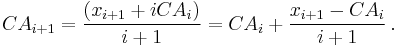
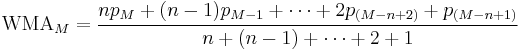
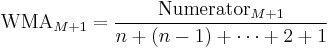
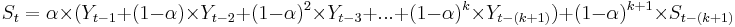
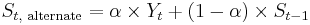
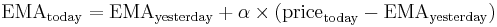
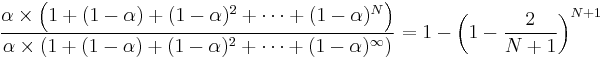
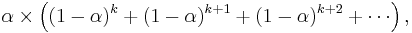
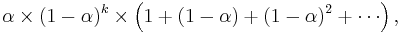
![{{\text{weight omitted by stopping after k terms}} \over {\text{total weight}}} = { { \alpha \times \left[ (1-\alpha)^k %2B(1-\alpha)^{k%2B1} %2B(1-\alpha)^{k%2B2} %2B \cdots \right] } \over { { \alpha \times \left[ 1 %2B (1-\alpha) %2B(1-\alpha)^{2} %2B \cdots \right] } } }](/2012-wikipedia_en_all_nopic_01_2012/I/b84b0c8aa3bd7d0c8efed09ad70892ea.png)