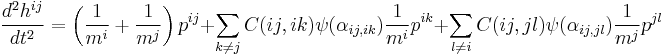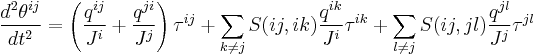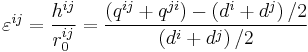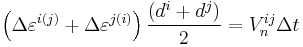Movable cellular automaton
Movable cellular automaton actively changed self neighbors by means switching neighbors state from linked to unlinked and vice versa (modeling of contact interaction) |
|
| Method type | |
|---|---|
| Continuous/Discrete | Discrete |
| Analytical/Computational | Computational |
| Characteristics | |
| Influenced by | cellular automaton, discrete element |
| Method in | computational solid mechanics |
The Movable cellular automaton (MCA) method is a method in computational solid mechanics based on the discrete concept. It provides advantages both of classical cellular automaton and discrete element methods. Important advantage of the МСА method is a possibility of direct simulation of materials fracture including damage generation, crack propagation, fragmentation and mass mixing. It is difficult to simulate these processes by means of continuum mechanics methods (For example: finite element method, finite difference method, etc.), so some new concepts like peridynamics is required. Discrete element method is very effective to simulate granular materials, but mutual forces among movable cellular automata provides simulating solids behavior. If size of automaton will be close to zero then MCA behavior becomes like classical continuum mechanics methods.
Keystone of the movable cellular automaton method
In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: Ri – radius-vector of automaton; Vi – velocity of automaton; ωi – rotation velocity of automaton; θi – rotation vector of automaton; mi – mass of automaton; Ji – moment of inertia of automaton.
New concept: neighbours
The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.
Definition of the parameter of pair state
The introducing of new type of states leads to new parameter to use it as criteria for switching relationships. It is defined as an automaton overlapping parameters hij. So the relationship of the cellular automata is characterised by the value of their overlapping.
The initial structure is formed by setting up certain relationships among each pair of neighboring elements.
Criterion of switching of the state of pair relationships
In contrast to the classical cellular automaton method in the MCA method not only a single automaton but also a relationship of pair of automata can be switched. According with the bistable automata concept there are two types of the pair states (relationships):
| linked | – both automata belong to a solid |
| unlinked | – each automaton of the pair belongs to different bodies or parts of damaged body. |
So the changing of the state of pair relationships is controlled by relative movements of the automata and the media formed by such pairs can be considered as bistable media.
Equations of MCA motion
The evolution of MCA media is described by the following equations of motion for translation:
Here mi is the mass of automaton i, pij is central force acting between automata i and j, C(ij,ik) is certain coefficient associated with transferring the h parameter from pair ij to pair ik, ψ(αij,ik) is angle between directions ij and ik.
Due to finite size of movable automata the rotation effects have to be taken into account. The equations of motion for rotation can be written as follows:
Here Θij is the angle of relative rotation (it is a switching parameter like hij for translation), qij is the distance from center of automaton i to contact point of automaton j (moment arm), τij is the pair tangential interaction, S(ij,ik) is certain coefficient associated with transferring the Θ parameter from one pair to other (it is similar to C(ij,ik) from the equation for translation).
It should be noted that these equations are completely similar to the equations of motion for the many–particle approach.
Definition of deformation in pair of automata
Translation of the pair automata The dimensionless deformation parameter for translation of the i j automata pair can be presented as:
In this case:
where Δt time step, Vnij – relative velocity.
Rotation of the pair automata can be calculated by analogy with the last translation relationships.
Modeling of irreversible deformation in the MCA method
The εij parameter is used as a measure of deformation of automaton i under its interaction with automaton j. Where qij – is a distance from the center of automaton i to its contact point with automaton j; Ri = di/2 (di – is the size of automaton i).
As an example the titanium specimen under cyclic loading (tension – compression) is considered. The loading diagram is shown in the next figure:
| Scheme of loading | Loading diagram |
|---|---|
| (Red marks are the experimental data) |
Advantages of MCA method
Due to mobility of each automaton the MCA method allows to take into account directly such actions as:
- mass mixing
- penetration effects
- chemical reactions
- intensive deformation
- phase transformations
- accumulation of damages
- fragmentation and fracture
- cracks generation and development
Using boundary conditions of different types (fixed, elastic, viscous-elastic, etc.) it is possible to imitate different properties of surrounding medium, containing the simulated system. It is possible to model different modes of mechanical loading (tension, compression, shear strain, etc.) by setting up additional conditions at the boundaries.
References
- Psakhie, S.G.; Horie, Y.; Korostelev, S.Yu.; Smolin, A.Yu.; Dmitriev, A.I.; Shilko, E.V.; Alekseev, S.V. (November. - 1995). "Method of movable cellular automata as a tool for simulation within the framework of mesomechanics". Russian Physics Journal (Springer New York) 38 (11): 1157–1168. doi:10.1007/BF00559396.
- Psakhie, S.G.; Korostelev, S.Y.; Smolin, A.Y.; Dmitriev, A.I.; Shilko, E.V.; Moiseenko D.D.; Tatarincev E.M.; Alekseev, S.V. (1998). "Movable cellular automata method as a tool for physical mesomechanics of materials". Physical mesomechanics (The Organization of the Russian Academy of Sciences, Institute of Strength Physics and Materials Science of the Siberian Branch of RAS (ISPMS SB RAS)) 1 (1): 95–108. (Russian: Псахье, С.Г.; Коростелев, С.Ю.; Смолин, А.Ю.; Дмитриев, А.И.; Шилько, Е.В.; Моисеенко, Д.Д.; Татаринцев, Е.М.; Алексеев, С.В. (1998). "Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов". Физическая мезомеханика (Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН)) 1 (1): 95–108. http://elibrary.ru/item.asp?id=12913617. Retrieved 2010-03-03.)
- Psakhie, S.G.; Ostermeyer, G.P.; Dmitriev, A.I.; Shilko, E.V.; Smolin, A.Y.; Korostelev, S.Y. (2000). "Movable cellular automata method as new direction in numerical discrete mechanics. I. Theoretical description". Physical mesomechanics (The Organization of the Russian Academy of Sciences, Institute of Strength Physics and Materials Science of the Siberian Branch of RAS (ISPMS SB RAS)) 3 (2): 5–13. (Russian: Псахье, С.Г.; Остермайер, Г.П.; Дмитриев, А.И.; Шилько, Е.В.; Смолин, А.Ю.; Коростелев, С.Ю. (2000). "Метод подвижных клеточных автоматов как новое направление дискретной вычислительной механики. I. Теоретическое описание". Физическая мезомеханика (Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН)) 3 (2): 5–13. http://elibrary.ru/item.asp?id=12913646. Retrieved 2010-03-03.)
- Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Yu.; Smolin, A.Yu.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S.; Spegel, M.; Zavsek, S. (December 2001). "Movable cellular automata method for simulating materials with mesostructure". Theoretical and Applied Fracture Mechanics (Elsevier Science Ltd.) 37 (1-3): 311–334. doi:10.1016/S0167-8442(01)00079-9. http://mechanik.tu-berlin.de/popov/software/mca/TAFMEC.pdf.
- Psakhie, S.G.; Smolin, A.Y.; Stefanov, Y.P.; Makarov, P.V.; Chertov, M.A. (2004). "Modeling the behavior of complex media by jointly using discrete and continuum approaches". Technical Physics Letters (MAIK Nauka/Interperiodica distributed exclusively by Springer Science+Business Media LLC.) 30 (9): 712–714. doi:10.1134/1.1804572.
- Shimizu, Y.; Hart, R.; Cundall, P. (2004). Numerical modeling in Micromechanics via Particle Methods. ISBN 9058096793. http://books.google.com/books?id=GVAUH98Yr6oC&lpg=PA242&dq=%22Movable%20cellular%20automaton%22%20-inpublisher%3Aicon&as_brr=0&hl=ru&pg=PR4#v=onepage&q=%22Movable%20cellular%20automaton%22%20-inpublisher:icon&f=false. Retrieved 2010-03-03.
- Gnecco, E.; Meyer E. (Eds.) (2007). Fundamentals of friction and wear on the Nanoscale. ISBN 9783540368069. http://books.google.com/books?id=v2Pe5thhNiwC&lpg=PP1&hl=ru&pg=PP1#v=onepage&q=&f=false. Retrieved 2010-03-03.
- Yunliang, Tan; Guirong, Teng; Haitao, Li. "MCA Model for Simulating the Failure of Microinhomogeneous Materials". Journal of Nanomaterials (Hindawi Publishing Corporation) 2008: 1–7. doi:10.1155/2008/946038. 946038.
- Fomin, V.M.; Andreev, A.N. and al (2008). Mechanics - from discrete to continious. Russian academy of science, Siberian branch, Institute of theoretical and applied mechanics (named S.A. Khristianovich). p. 344. ISBN 978-5-7692-0974-1. (Russian: Фомин, В.М.; Андреев А.Н. и др. (2008). Механика - от дискретного к сплошному. Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича. p. 344. ISBN 978-5-7692-0974-1. http://www.sibran.ru/psb/books/show_text.phtml?rus+1880+psb. Retrieved 3.03.2010.)
- Smolin, A.Y.; Roman, N.V.; Dobrynin, S.A.; Psakhie, S.G. (May-August. - 2009). "On rotation in the movable cellular automaton method". Physical Mesomechanics (Elsevier B.V.) 12 (3-4): 124–129. doi:10.1016/j.physme.2009.07.004.
- Popov, Valentin L. (2009). Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation). Springer Berlin Heidelberg. doi:10.1007/978-3-540-88837-6. ISBN 9783540888369.
- Dobrynin, S.A. (2010). Development of movable cellular atomaton method for modeling generation and propagation of elastic waves under contact interaction of solids. Tomsk: PhD thesis in physics and mathematics. p. 130. (Russian: Добрынин, С.А. (2010). Развитие метода подвижных клеточных автоматов для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел. Томск: Диссертация … кандидата физико-математических наук. p. 130. http://serg-dobrinin.narod.ru/disert/index.html. Retrieved 3.03.2010.)
- Dobrynin, Sergey (2011). Computer simulation by movable cellular automaton method. Saarbrücken Germany: LAP LAMBERT Academic Publishing. p. 132. ISBN 978-3-8443-5954-1. (Russian: Добрынин, Сергей (2011). Компьютерное моделирование методом подвижных клеточных автоматов. Saarbrücken Germany: LAP LAMBERT Academic Publishing. p. 132. ISBN 978-3-8443-5954-1. https://www.lap-publishing.com/catalog/details/store/gb/book/978-3-8443-5954-1/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%BE%D0%B5-%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%BE%D0%BC-%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D1%85-%D0%BA%D0%BB%D0%B5%D1%82%D0%BE%D1%87%D0%BD%D1%8B%D1%85-%D0%B0%D0%B2%D1%82%D0%BE%D0%BC%D0%B0%D1%82%D0%BE%D0%B2. Retrieved 19.11.2011.)
Software
- MCA software package
- Software for simulation of materials in discrete-continuous approach «FEM+MCA»: Number of state registration in Applied Research Foundation of Algorithms and Software (AFAS): 50208802297 / Smolin A.Y., Zelepugin S.A., Dobrynin S.A.; applicant and development center is Tomsk State University. – register date 28.11.2008; certificate AFAS N 11826 date 01.12.2008.