Mott insulator
Mott insulators are a class of materials that should conduct electricity under conventional band theories, but are insulators when measured (particularly at low temperatures). This effect is due to electron-electron interactions which are not considered in conventional band theory.
The bandgap in a Mott insulator exists between bands of like character, such as 3d character, while the bandgap in charge transfer insulators exists between anion and cation states (see lecture slides ), such as between O 2p and Ni 3d bands in NiO. [1]
Contents |
History
Although the band theory of solids had been very successful in describing various electrical properties of materials, in 1937 Jan Hendrik de Boer and Evert Johannes Willem Verwey pointed out that a variety of transition metal oxides predicted to be conductors by band theory (because they have an odd number of electrons per unit cell) are insulators.[2] Nevill Mott and R. Peierls then (also in 1937) predicted that this anomaly can be explained by including interactions between electrons.[3]
In 1949, in particular, Mott proposed a model for NiO as an insulator, where conduction is based on the formula[4]
- (Ni2+O2−)2 → Ni3+O2− + Ni1+O2−.
In this situation, the formation of an energy gap preventing conduction can be understood as the competition between the Coulomb potential U between 3d electrons and the transfer integral t of 3d electrons between neighboring atoms (the transfer integral is a part of the tight-binding approximation). The total energy gap is then
- Egap = U − 2zt,
where z is the number of nearest-neighbor atoms.
In general, Mott insulators occur when the repulsive Coulomb potential U is large enough to create an energy gap. One of the simplest theories of Mott insulators is the 1963 Hubbard model. The crossover from a metal to a Mott insulator as  is increased can be predicted within the so-called Dynamical Mean Field Theory.
is increased can be predicted within the so-called Dynamical Mean Field Theory.
Mottness
Mottness denotes the additional ingredient, aside from antiferromagnetic ordering, which is necessary to fully describe a Mott Insulator. In other words, we might write
- antiferromagnetic order + mottness = Mott insulator
Thus, mottness accounts for all of the properties of Mott insulators that cannot be attributed simply to antiferromagnetism.
There are a number of properties of Mott insulators, derived from both experimental and theoretical observations, which cannot be attributed to antiferromagnetic ordering and thus constitute mottness. These properties include
- Spectral weight transfer on the Mott scale [5][6]
- Vanishing of the single particle Green function along a connected surface in momentum space in the first brillouin zone [7]
- Two sign changes of the Hall coefficient as electron doping goes from
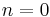 to
to 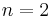 (band insulators have only one sign change at
(band insulators have only one sign change at 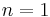 )
) - The presence of a charge
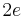 (with
(with 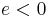 the charge of an electron) boson at low energies [8][9]
the charge of an electron) boson at low energies [8][9] - A pseudogap away from half-filling (
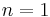 ) [10]
) [10]
Applications
Mott insulators are of growing interest in advanced physics research, and are not yet fully understood. They have applications in thin-film magnetic heterostructures and high-temperature superconductivity, for example.[11]
See also
- Hubbard model
- Tight-binding approximation
- Electronic band structure
- Mott Criterion
- Dynamical Mean Field Theory
- (Mott) Variable range hopping
References
- R.B. Laughlin, "A Critique of Two Metals," http://arxiv.org/abs/cond-mat/9709195
- Philip W. Anderson and G. Baskaran, "A Critique of 'A Critique of Two Metals,'" http://arxiv.org/abs/cond-mat/9711197
- ^ P. Kuiper, G. Gruizinga, J. Ghijsen, G.A. Sawatzky, H. Verweij (1987). "Character of Holes in LixNi1-xO2". Physical Review Letters 62 (2): 221–224. Bibcode 1989PhRvL..62..221K. doi:10.1103/PhysRevLett.62.221. PMID 10039954.
- ^ de Boer, J. H.; Verwey, E. J. W. (1937). "Semi-conductors with partially and with completely filled 3d-lattice bands". Proceedings of the Physical Society of London 49 (4S): 59. doi:10.1088/0959-5309/49/4S/307.
- ^ Mott, N. F.; Peierls, R. (1937). "Discussion of the paper by de Boer and Verwey". Proceedings of the Physical Society of London 49 (4S): 72. Bibcode 1937PPS....49...72M. doi:10.1088/0959-5309/49/4S/308.
- ^ Mott, N. F. (1949). "The basis of the electron theory of metals, with special reference to the transition metals". Proceedings of the Physical Society of London Series A 62 (7): 416. Bibcode 1949PPSA...62..416M. doi:10.1088/0370-1298/62/7/303.
- ^ Philip Phillips, "Mottness," http://arxiv.org/abs/cond-mat/0702348
- ^ M.B.J. Meinders, H. Eskes, and G.A. Sawatzky, Phys. Rev. B 48 3916 (1993)
- ^ Tudor D. Stanescu, Philip Phillips, and Ting-Pong Choy, "Theory of the Luttinger surface in doped Mott insulators," Phys. Rev. B 75 104503 (2007)
- ^ Robert G. Leigh, Philip Phillips, and Ting-Pong Choy, "Hidden Charge 2e Boson in Doped Mott Insulators: Field Theory of Mottness," to be published in Phys. Rev. Lett., http://arxiv.org/abs/cond-mat/0612130v3 (2007)
- ^ Ting-Pong Choy, Robert G. Leigh, Philip Phillips, and Philip D. Powell, "Exact Integration of the High Energy Scale in Doped Mott Insulators," http://arxiv.org/abs/0707.1554
- ^ Tudor D. Stanescu and Philip Phillips, "Pseudogap in Doped Mott Insulators is the Near-neighbour Analogue of the Mott Gap," Phys. Rev. Lett. 91, 017002 (2003), http://arxiv.org/abs/cond-mat/0209118
- ^ Kohsaka, Y.; Taylor, C.; Wahl, P.; et al. (August 28, 2008). "How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8+δ". Nature 454 (7208): 1072–1078. Bibcode 2008Natur.454.1072K. doi:10.1038/nature07243. PMID 18756248.