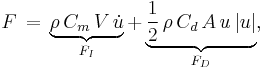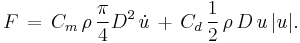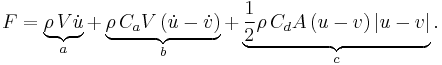Morison equation
In fluid dynamics the Morison equation is a semi-empirical equation for the inline force on a body in oscillatory flow. It is sometimes called the MOJS equation after all four authors—Morison, O'Brien, Johnson and Schaaf—of the 1950 paper in which the equation was introduced.[1] The Morison equation is used to estimate the wave loads in the design of oil platforms and other offshore structures.[2][3]
Contents |
Description
The Morison equation is the sum of two force components: an inertia force in phase with the local flow acceleration and a drag force proportional to the (signed) square of the instantaneous flow velocity. The inertia force is of the functional form as found in potential flow theory, while the drag force has the form as found for a body placed in a steady flow. In the heuristic approach of Morison, O'Brien, Johnson and Schaaf these two force components, inertia and drag, are simply added to describe the force in an oscillatory flow.
The Morison equation contains two empirical hydrodynamic coefficients—an inertia coefficient and a drag coefficient—which are determined from experimental data. As shown by dimensional analysis and in experiments by Sarpkaya, these coefficients depend in general on the Keulegan–Carpenter number, Reynolds number and surface roughness.[4][5]
The descriptions given below of the Morison equation are for uni-directional onflow conditions as well as body motion.
Fixed body in an oscillatory flow
In an oscillatory flow with flow velocity 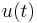 , the Morison equation gives the inline force parallel to the flow direction:[6]
, the Morison equation gives the inline force parallel to the flow direction:[6]
where
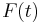 is the total inline force on the object,
is the total inline force on the object,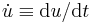 is the flow acceleration, i.e. the time derivative of the flow velocity
is the flow acceleration, i.e. the time derivative of the flow velocity 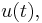
- the inertia force
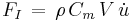 , is the sum of the Froude–Krylov force
, is the sum of the Froude–Krylov force 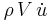 and the hydrodynamic mass force
and the hydrodynamic mass force 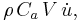
- the drag force
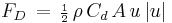 ,
, 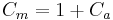 is the inertia coefficient, and
is the inertia coefficient, and 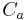 the added mass coefficient,
the added mass coefficient,- A is a reference area, e.g. the cross-sectional area of the body perpendicular to the flow direction,
- V is volume of the body.
For instance for a circular cylinder of diameter D in oscillatory flow, the reference area per unit cylinder length is 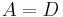 and the cylinder volume per unit cylinder length is
and the cylinder volume per unit cylinder length is 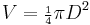 . As a result,
. As a result, 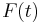 is the total force per unit cylinder length:
is the total force per unit cylinder length:
Besides the inline force, there are also oscillatory lift forces perpendicular to the flow direction, due to vortex shedding. These are not covered by the Morison equation, which is only for the inline forces.
Moving body in an oscillatory flow
In case the body moves as well, with velocity 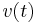 , the Morison equation becomes:[6]
, the Morison equation becomes:[6]
where the total force contributions are:
- a: Froude–Krylov force,
- b: hydrodynamic mass force,
- c: drag force.
Note that the added mass coefficient 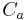 is related to the inertia coefficient
is related to the inertia coefficient 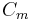 as
as 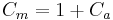 .
.
Limitations
- The Morison equation is a heuristic formulation of the force fluctuations in an oscillatory flow. The first assumption is that the flow acceleration is more-or-less uniform at the location of the body. For instance, for a vertical cylinder in surface gravity waves this requires that the diameter of the cylinder is much smaller than the wavelength. If the diameter of the body is not small compared to the wavelength, diffraction effects have to be taken into account.
- Second, it is assumed that the asymptotic forms: the inertia and drag force contributions, valid for very small and very large Keulegan–Carpenter numbers respectively, can just be added to describe the force fluctuations at intermediate Keulegan–Carpenter numbers. However, from experiments it is found that in this intermediate regime—where both drag and inertia are giving significant contributions—the Morison equation is not capable to describe the force history very well. Although the inertia and drag coefficients can be tuned to give the correct extreme values of the force.
- Third, when extended to orbital flow which is a case of non uni-directional flow, for instance encountered by a horizontal cylinder under waves, the Morison equation does not give a good representation of the forces as a function of time.[7]
See also
Notes
- ^ Sarpkaya, T. (1986), "Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers", Journal of Fluid Mechanics 165: 61–71, Bibcode 1986JFM...165...61S, doi:10.1017/S0022112086002999
- ^ Gudmestad, Ove T.; Moe, Geir (1996), "Hydrodynamic coefficients for calculation of hydrodynamic loads on offshore truss structures", Marine Structures 9 (8): 745–758, doi:10.1016/0951-8339(95)00023-2
- ^ "Guidelines on design and operation of wave energy converters". Det Norske Veritas. May 2005. http://www.dnv.no/Binaries/WECguideline_tcm28-181675.pdf. Retrieved 16-02-2009.
- ^ Sarpkaya, T. (1976), "Vortex shedding and resistance in harmonic flow about smooth and rough circular cylinders", Proceedings of the International Conference on the Behavior of Offshore Structures, BOSS '76, 1, pp. 220–235
- ^ Sarpkaya, T. (1977), Vortex shedding and resistance in harmonic flow about smooth and rough cylinders at high Reynolds numbers, Monterey: Naval Postgraduate School, Report No. NPS-59SL76021
- ^ a b Sumer & Fredsøe (2006), p. 131.
- ^ Chaplin, J. R. (1984), "Nonlinear forces on a horizontal cylinder beneath waves", Journal of Fluid Mechanics 147: 449–464, Bibcode 1984JFM...147..449C, doi:10.1017/S0022112084002160
References
- Morison, J. R.; O'Brien, M. P.; Johnson, J. W.; Schaaf, S. A. (1950), "The force exerted by surface waves on piles", Petroleum Transactions (American Institute of Mining Engineers) 189: 149–154
- Sarpkaya, T.; Isaacson, M. (1981), Mechanics of wave forces on offshore structures, New York: Van Nostrand Reinhold, ISBN 0442254024
- Sumer, B. M.; Fredsøe, J. (2006), Hydrodynamics around cylindrical structures, Advanced Series on Ocean Engineering, 26 (revised ed.), World Scientific, ISBN 9812700390, 530 pages