Moore–Penrose pseudoinverse
In mathematics, and in particular linear algebra, a pseudoinverse A+ of a matrix A is a generalization of the inverse matrix.[1] The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore[2] in 1920, Arne Bjerhammar [3] in 1951 and Roger Penrose[4] in 1955. Earlier, Fredholm had introduced the concept of a pseudoinverse of integral operators in 1903. When referred to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose pseudoinverse. The term generalized inverse is sometimes used as a synonym for pseudoinverse.
A common use of the Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) is to compute a 'best fit' (least squares) solution to a system of linear equations that lacks a unique solution (see below under Applications). Another use is to find the minimum (Euclidean) norm solution to a system of linear equations with multiple solutions. The pseudoinverse facilitates the statement and proof of results in linear algebra.
The pseudoinverse is defined and unique for all matrices whose entries are real or complex numbers. It can be computed using the singular value decomposition.
Contents |
Notation
In the following discussion, the following conventions are adopted.
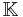 will denote one of the fields of real or complex numbers, denoted
will denote one of the fields of real or complex numbers, denoted 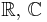 , respectively. The ring of
, respectively. The ring of 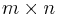 matrices over
matrices over 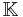 is denoted by
is denoted by 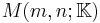 .
.- For
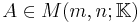 ,
, 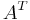 and
and 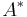 denote the transpose and Hermitian transpose (also called conjugate transpose) respectively. If
denote the transpose and Hermitian transpose (also called conjugate transpose) respectively. If 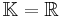 , then
, then 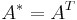 .
. - For
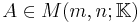 , then
, then 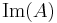 denotes the range (image) of
denotes the range (image) of  (the space spanned by the column vectors of
(the space spanned by the column vectors of  ) and
) and 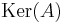 denotes the kernel (null space) of
denotes the kernel (null space) of  .
. - Finally, for any positive integer
 ,
, 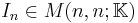 denotes the
denotes the 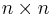 identity matrix.
identity matrix.
Definition
For 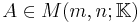 , a Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) of
, a Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) of  is defined as a matrix
is defined as a matrix 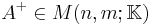 satisfying all of the following four criteria:[4][5]
satisfying all of the following four criteria:[4][5]
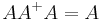 (AA+ need not be the general identity matrix, but it maps all column vectors of A to themselves);
(AA+ need not be the general identity matrix, but it maps all column vectors of A to themselves);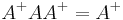 (A+ is a weak inverse for the multiplicative semigroup);
(A+ is a weak inverse for the multiplicative semigroup);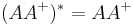 (AA+ is Hermitian); and
(AA+ is Hermitian); and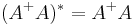 (A+A is also Hermitian).
(A+A is also Hermitian).
Properties
Proofs for some of these facts may be found on a separate page here.
Existence and uniqueness
- The Moore–Penrose pseudoinverse exists and is unique: for any matrix
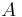 , there is precisely one matrix
, there is precisely one matrix 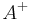 , that satisfies the four properties of the definition.[5]
, that satisfies the four properties of the definition.[5]
A matrix satisfying the first two conditions of the definition is known as a generalized inverse. Generalized inverses always exist but are not in general unique. Uniqueness is a consequence of the last two conditions.
Basic properties
- If
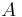 has real entries, then so does
has real entries, then so does 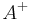 .
. - If
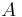 is invertible, the pseudoinverse and the inverse coincide:
is invertible, the pseudoinverse and the inverse coincide: 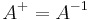 .[6]:243
.[6]:243 - The pseudoinverse of a zero matrix is its transpose.
- The pseudoinverse of the pseudoinverse is the original matrix:
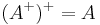 .[6]:245
.[6]:245 - Pseudoinversion commutes with transposition, conjugation, and taking the conjugate transpose:[6]:245
- The pseudoinverse of a scalar multiple of A is the reciprocal multiple of A+:
-
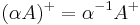 for
for 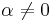 .
.
Identities
The following identities can be used to cancel certain subexpressions or expand expressions involving pseudoinverses. Proofs for these properties can be found in the proofs subpage.
Reduction to Hermitian case
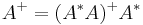 .
.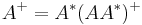 .
.
Products
If 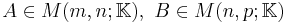 and either,
and either,
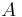 has orthonormal columns (i.e.
has orthonormal columns (i.e. 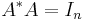 ) or,
) or,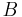 has orthonormal rows (i.e.
has orthonormal rows (i.e. 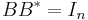 ) or,
) or,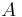 has all columns linearly independent (full column rank) and
has all columns linearly independent (full column rank) and 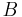 has all rows linearly independent (full row rank),
has all rows linearly independent (full row rank),
then 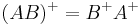 .
.
Projectors
If 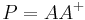 and
and 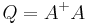 are orthogonal projection operators --- that is, they are Hermitian (
are orthogonal projection operators --- that is, they are Hermitian (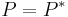 ,
, 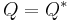 ) and idempotent (
) and idempotent (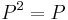 and
and 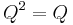 ) --- then the following hold:
) --- then the following hold:
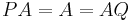 and
and 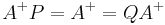
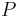 is the orthogonal projector onto the range of
is the orthogonal projector onto the range of 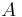 (which equals the orthogonal complement of the kernel of
(which equals the orthogonal complement of the kernel of 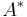 ).
).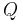 is the orthogonal projector onto the range of
is the orthogonal projector onto the range of 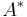 (which equals the orthogonal complement of the kernel of
(which equals the orthogonal complement of the kernel of 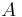 ).
).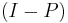 is the orthogonal projector onto the kernel of
is the orthogonal projector onto the kernel of 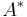 .
.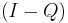 is the orthogonal projector onto the kernel of
is the orthogonal projector onto the kernel of 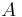 .[5]
.[5]
Subspaces
Limit relations
- The pseudoinverse are limits:
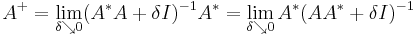
- (see Tikhonov regularization). These limits exist even if
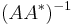 or
or 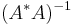 do not exist.[5]:263
do not exist.[5]:263
Continuity
- In contrast to ordinary matrix inversion, the process of taking pseudoinverses is not continuous: if the sequence
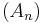 converges to the matrix A (in the maximum norm or Frobenius norm, say), then (An)+ need not converge to A+. However, if all the matrices have the same rank, (An)+ will converge to A+.
converges to the matrix A (in the maximum norm or Frobenius norm, say), then (An)+ need not converge to A+. However, if all the matrices have the same rank, (An)+ will converge to A+.
Special cases
Scalars
It is also possible to define a pseudoinverse for scalars and vectors. This amounts to treating these as matrices. The pseudoinverse of a scalar x is zero if x is zero and the reciprocal of x otherwise:
Vectors
The pseudoinverse of the null (all zero) vector is the transposed null vector. The pseudoinverse of a non-null vector is the conjugate transposed vector divided by its squared magnitude:
Linearly independent columns
If the columns of 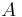 are linearly independent (so that
are linearly independent (so that 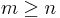 ), then
), then 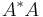 is invertible. In this case, an explicit formula is:[1]
is invertible. In this case, an explicit formula is:[1]
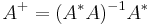 .
.
It follows that 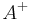 is then a left inverse of
is then a left inverse of 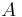 :
: 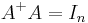 .
.
Linearly independent rows
If the rows of 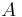 are linearly independent (so that
are linearly independent (so that 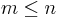 ), then
), then 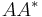 is invertible. In this case, an explicit formula is:
is invertible. In this case, an explicit formula is:
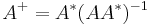 .
.
It follows that 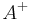 is a right inverse of
is a right inverse of 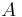 :
: 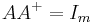 .
.
Orthonormal columns or rows
This is a special case of either full column rank or full row rank (treated above). If 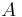 has orthonormal columns (
has orthonormal columns (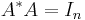 ) or orthonormal rows (
) or orthonormal rows (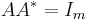 ), then
), then 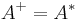 .
.
Circulant matrices
For a Circulant matrix 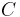 , the singular value decomposition is given by the Fourier transform, that is the singular values are the Fourier coefficients. Let
, the singular value decomposition is given by the Fourier transform, that is the singular values are the Fourier coefficients. Let 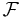 be the Discrete Fourier Transform (DFT) matrix, then
be the Discrete Fourier Transform (DFT) matrix, then
Construction
Rank decomposition
Let 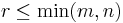 denote the rank of
denote the rank of 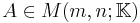 . Then
. Then 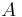 can be (rank) decomposed as
can be (rank) decomposed as 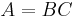 where
where 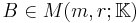 and
and 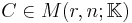 are of rank
are of rank  . Then
. Then 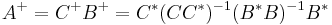 .
.
The QR method
For 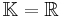 or
or 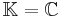 computing the product
computing the product 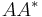 or
or 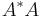 and their inverses explicitly is often a source of numerical rounding errors and computational cost in practice. An alternative approach using the QR decomposition of
and their inverses explicitly is often a source of numerical rounding errors and computational cost in practice. An alternative approach using the QR decomposition of 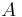 may be used instead.
may be used instead.
Considering the case when 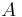 is of full column rank, so that
is of full column rank, so that 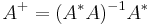 . then the Cholesky decomposition
. then the Cholesky decomposition 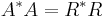 , where
, where 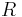 is an upper triangular matrix, may be used. Multiplication by the inverse is then done easily by solving a system with multiple right-hand-sides,
is an upper triangular matrix, may be used. Multiplication by the inverse is then done easily by solving a system with multiple right-hand-sides,
which may be solved by forward substitution followed by back substitution.
The Cholesky decomposition may be computed without forming 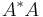 explicitly, by alternatively using the QR decomposition of
explicitly, by alternatively using the QR decomposition of 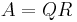 , where
, where 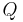 has orthonormal columns,
has orthonormal columns, 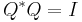 , and
, and 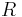 is upper triangular. Then
is upper triangular. Then
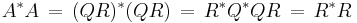 ,
,
so R is the Cholesky factor of 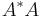 .
.
The case of full row rank is treated similarly by using the formula 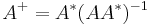 and using a similar argument, swapping the roles of
and using a similar argument, swapping the roles of  and
and 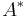 .
.
Singular value decomposition (SVD)
A computationally simple and accurate way to compute the pseudoinverse is by using the singular value decomposition.[1][5][8] If 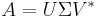 is the singular value decomposition of A, then
is the singular value decomposition of A, then 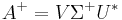 . For a diagonal matrix such as
. For a diagonal matrix such as 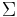 , we get the pseudoinverse by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and transposing the resulting matrix. In numerical computation, only elements larger than some small tolerance are taken to be nonzero, and the others are replaced by zeros. For example, in the MATLAB or NumPy function pinv, the tolerance is taken to be t = ε•max(m,n)•max(Σ), where ε is the machine epsilon.
, we get the pseudoinverse by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and transposing the resulting matrix. In numerical computation, only elements larger than some small tolerance are taken to be nonzero, and the others are replaced by zeros. For example, in the MATLAB or NumPy function pinv, the tolerance is taken to be t = ε•max(m,n)•max(Σ), where ε is the machine epsilon.
The computational cost of this method is dominated by the cost of computing the SVD, which is several times higher than matrix-matrix multiplication, even if a state-of-the art implementation (such as that of LAPACK) is used.
The above procedure shows why taking the pseudoinverse is not a continuous operation: if the original matrix A has a singular value 0 (a diagonal entry of the matrix 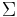 above), then modifying A slightly may turn this zero into a tiny positive number, thereby affecting the pseudoinverse dramatically as we now have to take the reciprocal of a tiny number.
above), then modifying A slightly may turn this zero into a tiny positive number, thereby affecting the pseudoinverse dramatically as we now have to take the reciprocal of a tiny number.
Block matrices
Optimized approaches exist for calculating the pseudoinverse of block structured matrices.
The iterative method of Ben-Israel and Cohen
Another method for computing the pseudoinverse uses the recursion
which is sometimes referred to as hyper-power sequence. This recursion produces a sequence converging quadratically to the pseudoinverse of  if it is started with an appropriate
if it is started with an appropriate 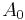 satisfying
satisfying 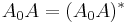 . The choice
. The choice 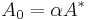 (where
(where 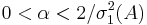 , with
, with 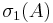 denoting the largest singular value of
denoting the largest singular value of  ) [9] has been argued not to be competitive to the method using the SVD mentioned above, because even for moderately ill-conditioned matrices it takes a long time before
) [9] has been argued not to be competitive to the method using the SVD mentioned above, because even for moderately ill-conditioned matrices it takes a long time before 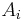 enters the region of quadratic convergence.[10] However, if started with
enters the region of quadratic convergence.[10] However, if started with 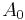 already close to the Moore–Penrose pseudoinverse and
already close to the Moore–Penrose pseudoinverse and 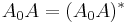 , for example
, for example 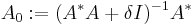 , convergence is fast (quadratic).
, convergence is fast (quadratic).
Updating the pseudoinverse
For the cases where A has full row or column rank, and the inverse of the correlation matrix (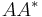 for A with full row rank or
for A with full row rank or 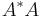 for full column rank) is already known, the pseudoinverse for matrices related to
for full column rank) is already known, the pseudoinverse for matrices related to  can be computed by applying the Sherman–Morrison–Woodbury formula to update the inverse of the correlation matrix, which may need less work. In particular, if the related matrix differs from the original one by only a changed, added or deleted row or column, incremental algorithms[11][12] exist that exploit the relationship.
can be computed by applying the Sherman–Morrison–Woodbury formula to update the inverse of the correlation matrix, which may need less work. In particular, if the related matrix differs from the original one by only a changed, added or deleted row or column, incremental algorithms[11][12] exist that exploit the relationship.
Similarly, it is possible to update the Cholesky factor when a row or column is added, without creating the inverse of the correlation matrix explicitly. However, updating the pseudoinverse in the general rank-deficient case is much more complicated.[13][14]
Software libraries
The package NumPy provides a pseudo-inverse calculation through its functions matrix.I and linalg.pinv. High quality implementations of SVD, QR, and back substitution are available in standard libraries, such as LAPACK. Writing one's own implementation of SVD is a major programming project that requires a significant numerical expertise. In special circumstances, such as parallel computing or embedded computing, however, alternative implementations by QR or even the use of an explicit inverse might be preferable, and custom implementations may be unavoidable.
Applications
Linear least-squares
The pseudoinverse provides a least squares solution to a system of linear equations.[15] For 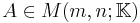 , given a system of linear equations
, given a system of linear equations
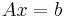 ,
,
in general, a vector  which solves the system may not exist, or if one exists, it may not be unique. The pseudoinverse solves the "least-squares" problem as follows:
which solves the system may not exist, or if one exists, it may not be unique. The pseudoinverse solves the "least-squares" problem as follows:
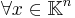 , we have
, we have 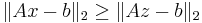 where
where 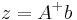 and
and 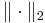 denotes the Euclidean norm. This weak inequality holds with equality if and only if
denotes the Euclidean norm. This weak inequality holds with equality if and only if 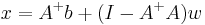 for any vector w; this provides an infinitude of minimizing solutions unless A has full column rank, in which case
for any vector w; this provides an infinitude of minimizing solutions unless A has full column rank, in which case 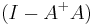 is a zero matrix.
is a zero matrix.
This result is easily extended to systems with multiple right-hand sides, when the Euclidean norm is replaced by the Frobenius norm. Let 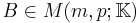 .
.
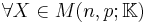 , we have
, we have 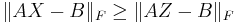 where
where 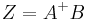 and
and 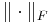 denotes the Frobenius norm.
denotes the Frobenius norm.
Obtaining all solutions of a linear system
If the linear system
has any solutions, they are all given by
for arbitrary vector w. Solution(s) exist if and only if 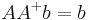 . If the latter holds, then the solution is unique if and only if A has full column rank, in which case
. If the latter holds, then the solution is unique if and only if A has full column rank, in which case ![[I - A^%2B A]](/2012-wikipedia_en_all_nopic_01_2012/I/c1ded8b0da60459302bcbe0e105d2241.png) is a zero matrix.
is a zero matrix.
Minimum-norm solution to a linear system
For linear systems 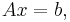 with non-unique solutions (such as under-determined systems), the pseudoinverse may be used to construct the solution of minimum Euclidean norm
with non-unique solutions (such as under-determined systems), the pseudoinverse may be used to construct the solution of minimum Euclidean norm 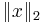 among all solutions.
among all solutions.
- If
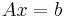 is satisfiable, the vector
is satisfiable, the vector 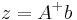 is a solution, and satisfies
is a solution, and satisfies 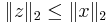 for all solutions.
for all solutions.
This result is easily extended to systems with multiple right-hand sides, when the Euclidean norm is replaced by the Frobenius norm. Let 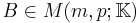 .
.
- If
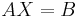 is satisfiable, the matrix
is satisfiable, the matrix 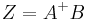 is a solution, and satisfies
is a solution, and satisfies 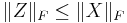 for all solutions.
for all solutions.
Geometric construction
This description suggests the following geometric construction for the result of applying the pseudoinverse of an m×n matrix A to a vector. To find 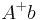 for given b in Rm, first project b orthogonally onto the range of A, finding a point p(b) in the range. Then form A-1({p(b)}), i.e. find those vectors in Rn that A sends to p(b). This will be an affine subspace of Rn parallel to the kernel of A. The element of this subspace that has the smallest length (i.e. is closest to the origin) is the answer
for given b in Rm, first project b orthogonally onto the range of A, finding a point p(b) in the range. Then form A-1({p(b)}), i.e. find those vectors in Rn that A sends to p(b). This will be an affine subspace of Rn parallel to the kernel of A. The element of this subspace that has the smallest length (i.e. is closest to the origin) is the answer 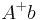 we are looking for. It can be found by taking an arbitrary member of A-1({p(b)}) and projecting it orthogonally onto the orthogonal complement of the kernel of A.
we are looking for. It can be found by taking an arbitrary member of A-1({p(b)}) and projecting it orthogonally onto the orthogonal complement of the kernel of A.
Condition number
Using the pseudoinverse and a matrix norm, one can define a condition number for any matrix:
A large condition number implies that the problem of finding least-squares solutions to the corresponding system of linear equations is ill-conditioned in the sense that small errors in the entries of A can lead to huge errors in the entries of the solution.[16]
Generalizations
In order to solve more general least-squares problems, one could try to define Moore–Penrose pseudoinverses for all continuous linear operators A : H1 → H2 between two Hilbert spaces H1 and H2, using the same four conditions as in our definition above. It turns out that not every continuous linear operator has a continuous linear pseudo-inverse in this sense.[16] Those that do are precisely the ones whose range is closed in H2.
In abstract algebra, a Moore–Penrose pseudoinverse may be defined on a *-regular semigroup. This abstract definition coincides with the one in linear algebra.
See also
- Proofs involving the Moore–Penrose pseudoinverse
- Drazin inverse
- Hat matrix
- Inverse element
- Linear least squares
- Pseudo-determinant
- Von Neumann regular ring
References
- ^ a b c Ben-Israel, Adi; Thomas N.E. Greville (2003). Generalized Inverses. Springer-Verlag. ISBN 0-387-00293-6.
- ^ Moore, E. H. (1920). "On the reciprocal of the general algebraic matrix". Bulletin of the American Mathematical Society 26 (9): 394–395. doi:10.1090/S0002-9904-1920-03322-7. http://projecteuclid.org/euclid.bams/1183425340.
- ^ Bjerhammar, Arne (1951). "Application of calculus of matrices to method of least squares; with special references to geodetic calculations". Trans. Roy. Inst. Tech. Stockholm 49.
- ^ a b Penrose, Roger (1955). "A generalized inverse for matrices". Proceedings of the Cambridge Philosophical Society 51: 406–413. doi:10.1017/S0305004100030401.
- ^ a b c d e Golub, Gene H.; Charles F. Van Loan (1996). Matrix computations (3rd ed.). Baltimore: Johns Hopkins. pp. 257–258. ISBN 0-8018-5414-8.
- ^ a b c Stoer, Josef; Bulirsch, Roland (2002). Introduction to Numerical Analysis (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-387-95452-3..
- ^ Stallings, W. T.; Boullion, T. L. (1972). "The Pseudoinverse of an r-Circulant Matrix". Proceedings of the American Mathematical Society 34: 385–388. doi:10.2307/2038377.
- ^ Linear Systems & Pseudo-Inverse
- ^ Ben-Israel, Adi; Cohen, Dan (1966). "On Iterative Computation of Generalized Inverses and Associated Projections". SIAM Journal on Numerical Analysis 3: 410–419. doi:10.1137/0703035. JSTOR 2949637.pdf
- ^ Söderström, Torsten; Stewart, G. W. (1974). "On the Numerical Properties of an Iterative Method for Computing the Moore- Penrose Generalized Inverse". SIAM Journal on Numerical Analysis 11: 61–74. doi:10.1137/0711008. JSTOR 2156431.
- ^ Tino Gramß (1992). Worterkennung mit einem künstlichen neuronalen Netzwerk. Georg-August-Universität zu Göttingen.
- ^ , Mohammad Emtiyaz, "Updating Inverse of a Matrix When a Column is Added/Removed"[1]
- ^ Meyer, Carl D., Jr. Generalized inverses and ranks of block matrices. SIAM J. Appl. Math. 25 (1973), 597—602
- ^ Meyer, Carl D., Jr. Generalized inversion of modified matrices. SIAM J. Appl. Math. 24 (1973), 315—323
- ^ Penrose, Roger (1956). "On best approximate solution of linear matrix equations". Proceedings of the Cambridge Philosophical Society 52: 17–19. doi:10.1017/S0305004100030929.
- ^ a b Roland Hagen, Steffen Roch, Bernd Silbermann. C*-algebras and Numerical Analysis, CRC Press, 2001. Section 2.1.2.
External links
- Pseudoinverse on PlanetMath
- Interactive program & tutorial of Moore-Penrose Pseudoinverse
- Moore-Penrose inverse on PlanetMath
- Weisstein, Eric W., "Pseudoinverse" from MathWorld.
- Weisstein, Eric W., "Moore-Penrose Inverse" from MathWorld.
|
||||||||||||||
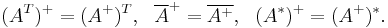
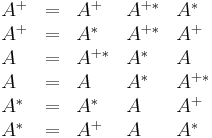
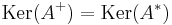
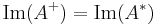
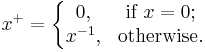
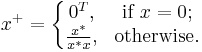
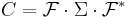
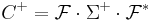
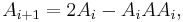
![x = A^%2B b %2B [I - A^%2B A]w](/2012-wikipedia_en_all_nopic_01_2012/I/5315141a1f75a6ed7727f46dd91c53a3.png)