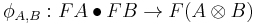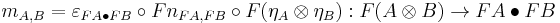Monoidal functor
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors:
- The coherence maps of lax monoidal functors satisfy no additional properties; they are not necessarily invertible.
- The coherence maps of strong monoidal functors are invertible.
- The coherence maps of strict monoidal functors are identity maps.
Although we distinguish between these different definitions here, authors may call any one of these simply monoidal functors.
Contents |
Definition
Let  and
and  be monoidal categories. A monoidal functor from
be monoidal categories. A monoidal functor from 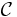 to
to 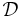 consists of a functor
consists of a functor 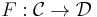 together with a natural transformation
together with a natural transformation
and a morphism
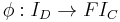 ,
,
called the coherence maps or structure morphisms, which are such that for every three objects  ,
,  and
and  of
of 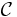 the diagrams
the diagrams
- ,
- and
commute in the category 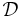 . Above, the various natural transformations denoted using
. Above, the various natural transformations denoted using 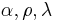 are parts of the monoidal structure on
are parts of the monoidal structure on 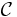 and
and 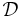 .
.
Variants
- The dual of a monoidal functor is a comonoidal functor; it is a monoidal functor whose coherence maps are reversed. Comonoidal functors may also be called opmonoidal, colax monoidal, or oplax monoidal functors.
- A strong monoidal functor is a monoidal functor whose coherence maps
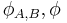 are invertible.
are invertible. - A strict monoidal functor is a monoidal functor whose coherence maps are identities.
- A braided monoidal functor is a monoidal functor between braided monoidal categories such that the following diagram commutes for every pair of objects A, B in
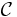 :
:
- A symmetric monoidal functor is a braided monoidal functor whose domain and codomain are symmetric monoidal categories.
Properties
Example
The underlying functor 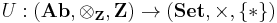 from the category of abelian groups to the category of sets. In this case, the map
from the category of abelian groups to the category of sets. In this case, the map 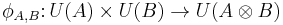 is a surjection induced by the bilinearity relation, i.e.
is a surjection induced by the bilinearity relation, i.e. 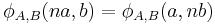 for
for 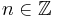 ; the map
; the map 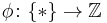 sends * to 1.
sends * to 1.
Monoidal functors and adjunctions
Suppose that a functor 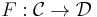 is left adjoint to a monoidal
is left adjoint to a monoidal 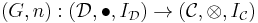 . Then
. Then  has a comonoidal structure
has a comonoidal structure 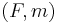 induced by
induced by 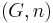 , defined by
, defined by
and
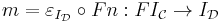 .
.
If the induced structure on  is strong, then the unit and counit of the adjunction are monoidal natural transformations, and the adjunction is said to be a monoidal adjunction; conversely, the left adjoint of a monoidal adjunction is always a strong monoidal functor.
is strong, then the unit and counit of the adjunction are monoidal natural transformations, and the adjunction is said to be a monoidal adjunction; conversely, the left adjoint of a monoidal adjunction is always a strong monoidal functor.
Similarly, a right adjoint to a comonoidal functor is monoidal, and the right adjoint of a comonoidal adjunction is a strong monoidal functor.
See also
References
- Kelly, G. Max (1974), "Doctrinal adjunction", Lecture Notes in Mathematics, 420, 257–280