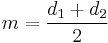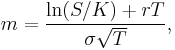Moneyness

"In the money" redirects here; for the poker term, see In the money (poker).

In finance, moneyness is a measure of the degree to which a derivative is likely to have positive monetary value at its expiration, in the risk-neutral measure. It can be measured in percentage probability, or in standard deviations.

Contents

Intrinsic value and time value

The intrinsic value (or "monetary value") of an option is the value of exercising it now. Thus if the current (spot) price of the underlying security is above the agreed (strike) price, a call has positive intrinsic value (and is called "in the money"), while a put has zero intrinsic value.

The time value of an option is a function of the option value less the intrinsic value. It equates to uncertainty in the form of investor hope. It is also viewed as the value of not exercising the option immediately. In the case of a European option, you cannot choose to exercise it at any time, so the time value can be negative; for an American option if the time value is ever negative, you exercise it: this yields a boundary condition.

ATM: At-the-money

An option is at-the-money if the strike price is the same as the spot price of the underlying security on which the option is written. An at-the-money option has no intrinsic value, only time value.

ITM: In-the-money

An in-the-money option has positive intrinsic value as well as time value. A call option is in-the-money when the strike price is below the spot price. A put option is in-the-money when the strike price is above the spot price.

OTM: Out-of-the-money

An out-of-the-money option has no intrinsic value. A call option is out-of-the-money when the strike price is above the spot price of the underlying security. A put option is out-of-the-money when the strike price is below the spot price.

Spot versus forward

Assets can have a forward price (a price for delivery in future) as well as a spot price. One can also talk about moneyness with respect to the forward price: thus one talks about ATMF, "ATM Forward", and so forth. For instance, if the spot price for USD/JPY is 120, and the forward price one year hence is 110, then a call struck at 110 is ATMF but not ATM.

Which are used?

Buying an ITM option is effectively lending money in the amount of the intrinsic value. Further, an ITM call can be replicated by entering a forward and buying an OTM put (and conversely). Consequently, ATM and OTM options are the main traded ones.

Example

Suppose the current stock price of IBM is $100. A call or put option with a strike of $100 is at-the-money. A call option with a strike of $80 is in-the-money (100 – 80 = 20 > 0). A put option with a strike at $80 is out-of-the-money (80 – 100 = –20 < 0). Conversely, a call option with a $120 strike is out-of-the-money and a put option with a $120 strike is in-the-money.

When one uses the Black–Scholes model to value the option, one may define moneyness quantitatively. If we define the moneyness (of a call) as

m = \frac{d_1%2Bd_2}{2}

where d1 and d2 are the standard Black–Scholes parameters then

m = \frac{\ln(S/K)%2BrT}{\sigma\sqrt T},

where T is the time to expiry.

In other words, it is the number of standard deviations the current price is above the ATMF price.

This choice of parameterisation means that the moneyness is zero when the forward price of the underlying, discounted at the risk-free rate, equals the strike price. Such an option is often referred to as at-the-money-forward. Moneyness is measured in standard deviations from this point, with a positive value meaning an in-the-money call option and a negative value meaning an out-of-the-money call option (with signs reversed for a put option).

One can also measure it as a percent, via 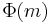\Phi(m), where 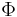\Phi is the standard normal cumulative distribution function; thus a moneyness of 0 yields a 50% probability of expiring ITM, while a moneyness of 1 yields an approximately 84% probability of expiring ITM.

Beware that (percentage) moneyness is close to but different from Delta: 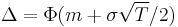\Delta = \Phi(m%2B\sigma\sqrt{T}/2) instead of 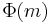\Phi(m), for a call (conversely for a put).

Thus a 25 Delta call option has approximately (but not exactly) 25% moneyness.

Note that r is the risk-free rate, not the expected return on the underlying.

References

Options
Terms
Swaps
Forwards and Futures
Other derivatives
Market issues