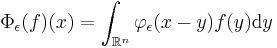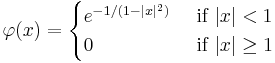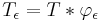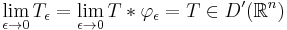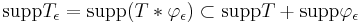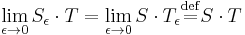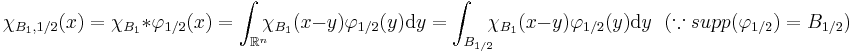Mollifier
In mathematics, mollifiers (also known as approximations to the identity) are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth (generalized) functions, via convolution. Intuitively, given a function which is rather irregular, by convolving it with a mollifier the function gets "mollified", that is, its sharp features are smoothed, while still remaining close to the original nonsmooth function. They are also known as Friedrichs mollifiers after Kurt Otto Friedrichs, the mathematician who introduced them.
Contents |
History
Mollifiers were introduced by Kurt Otto Friedrichs in his paper Friedrichs 1944, pp. 136–139, which is a watershed in the modern theory of partial differential equations.[1] The name of the concept had a curious genesis:[1] at that time Friedrichs was a colleague of the mathematician Donald Alexander Flanders, and since he liked to consult colleagues about English usage, he asked Flanders how to name the smoothing operator he was about to introduce.[2] Flanders was a puritan so his friends nicknamed him Moll after Moll Flanders in recognition of his moral qualities, and he suggested to call the new mathematical concept a "mollifier" as a pun incorporating both Flanders' nickname and the verb 'to mollify', meaning 'to smooth over' in a figurative sense.
Sergei Sobolev had previously used mollifiers in his epoch making 1938 paper containing the proof of the Sobolev embedding theorem,[3] as Friedrichs himself later acknowledged.[4]
There is a little misunderstanding in the concept of mollifier: Friedrichs defined as "mollifier" the integral operator whose kernel is one of the functions nowadays called mollifiers. However, since the properties of an integral operator are completely determined by its kernel, the name mollfier was inherited by the kernel itself as a result of common usage.
Definition
Modern (distribution based) definition
. If  is a smooth function on ℝn, n ≥ 1, satisfying the following three requirements
is a smooth function on ℝn, n ≥ 1, satisfying the following three requirements
- it is compactly supported (such as a bump function)
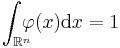
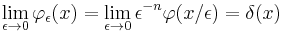
where 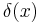 is the Dirac delta function and the limit must be understood in the space of Schwartz distributions, then
is the Dirac delta function and the limit must be understood in the space of Schwartz distributions, then  is a mollifier. The function
is a mollifier. The function  could satisfy also further conditions:[5] for example, if it satisfies
could satisfy also further conditions:[5] for example, if it satisfies

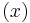 ≥ 0 for all x ∈ ℝn, then it is a positive mollifier
≥ 0 for all x ∈ ℝn, then it is a positive mollifier
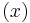 =
=
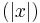 for some infinitely differentiable function
for some infinitely differentiable function  : ℝ+ → ℝ, then it is a symmetric mollifier
: ℝ+ → ℝ, then it is a symmetric mollifier
Notes on Friedrichs' definition
Note 1. When the theory of distributions was still not widely known nor used,[6] property (3) above was formulated by saying that the convolution of the function 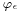 with a given function belonging to a proper Hilbert or Banach space converges as ε → 0 to this last one:[7] this is exactly what Friedrichs did.[8] This also clarifies why mollifiers are related to approximate identities.[9]
with a given function belonging to a proper Hilbert or Banach space converges as ε → 0 to this last one:[7] this is exactly what Friedrichs did.[8] This also clarifies why mollifiers are related to approximate identities.[9]
Note 2. As briefly pointed out in the "History" section of this entry, originally, the term "mollifier" identified the following convolution operator:[9][10]
where 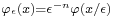 and
and  is a smooth function satisfying the first three conditions stated above and one or more supplementary conditions as positivity and symmetry.
is a smooth function satisfying the first three conditions stated above and one or more supplementary conditions as positivity and symmetry.
Concrete example
Consider the function 
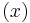 of the variable ℝn defined by
of the variable ℝn defined by
It is easily seen that this function is infinitely differentiable, non analytic with vanishing derivative for 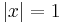 . Divide this function by its integral over the whole space to get a function
. Divide this function by its integral over the whole space to get a function  of integral one, which can be used as mollifier as described above: it is also easy to see that
of integral one, which can be used as mollifier as described above: it is also easy to see that 
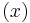 defines a positive and symmetric mollifier.[11]
defines a positive and symmetric mollifier.[11]
Properties
All properties of a mollifier are related to its behaviour under the operation of convolution: we list the following ones, whose proofs can be found in every text on distribution theory.[12]
Smoothing property
For any distribution  , the following sequence of convolutions indexed by the real number
, the following sequence of convolutions indexed by the real number 
where  denotes convolution, is a sequence of smooth functions.
denotes convolution, is a sequence of smooth functions.
Approximation of identity
For any distribution  , the following sequence of convolutions indexed by the real number
, the following sequence of convolutions indexed by the real number  converges to
converges to 
Support of convolution
For any distribution  ,
,
where 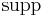 indicates the support in the sense of distributions, and
indicates the support in the sense of distributions, and 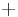 indicates their Minkowski addition.
indicates their Minkowski addition.
Applications
The basic applications of mollifiers is to prove properties valid for smooth functions also in nonsmooth situations:
Product of distributions
In some theories of generalized functions, mollifiers are used to define the multiplication of distributions: precisely, given two distributions  and
and  , the limit of the product of a smooth function and a distribution
, the limit of the product of a smooth function and a distribution
defines (if it exists) their product in various theories of generalized functions.
"Weak=Strong" theorems
Very informally, mollifiers are used to prove the identity of two different kind of extension of differential operators: the strong extension and the weak extension. The paper Friedrichs 1944 illustrates this concept quite well: however the high quantity of technical details needed to show what this really means prevent us from being formally detailed in this short description.
Smooth cutoff functions
By convolution of the characteristic function of the unit ball 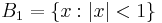 with the smooth function
with the smooth function 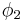 (defined as in (3) with
(defined as in (3) with 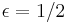 ), one obtains the function
), one obtains the function
which is a smooth function equal to 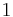 on
on 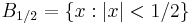 , with support contained in
, with support contained in 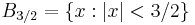 . This can be seen easily by observing that if
. This can be seen easily by observing that if 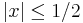 and
and 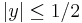 then
then 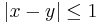 . Hence for
. Hence for 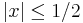 ,
,
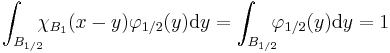 .
.
It is easy to see how this construction can be generalized to obtain a smooth function identical to one on a neighbourhood of a given compact set, and equal to zero in every point whose distance from this set is greater than a given  .[13] Such a function is called a (smooth) cutoff function: those functions are used to eliminate singularities of a given (generalized) function by multiplication. They leave unchanged the value of the (generalized) function they multiply only on a given set, thus modifying its support: also cutoff functions are the basic parts of smooth partitions of unity.
.[13] Such a function is called a (smooth) cutoff function: those functions are used to eliminate singularities of a given (generalized) function by multiplication. They leave unchanged the value of the (generalized) function they multiply only on a given set, thus modifying its support: also cutoff functions are the basic parts of smooth partitions of unity.
See also
- Approximate identity
- Bump function
- Convolution
- Distribution (mathematics)
- Kurt Otto Friedrichs
- Generalized function
- Sergei Sobolev
Notes
- ^ a b According to Peter Lax in Friedrichs 1986, p. 117, volume 1,
- ^ He introduced the term "Mollifier" in the paper Friedrichs 1944, as previously pointed out.
- ^ See Sobolev 1938
- ^ Precisely he acknowledged this fact in the paper Friedrichs 1953, p. 196
- ^ See Giusti 1984, p. 11.
- ^ as in the paper Friedrichs 1944, written few years before Laurent Schwartz widespread his work.
- ^ Obviously the topology with respect to convergence occurs is the one of the Hilbert or Banach space considered.
- ^ See (Friedrichs 1944, pp. 136–138), propeties PI, PII, PIII and their consequence PIII0.
- ^ a b Also, in this respect, Friedrichs (1944, pp. 132) says:-"The main tool for the proof is a certain class of smoothing operators approximating unity, the “mollifiers”".
- ^ See (Friedrichs 1944, p. 137), paragraph 2, "Integral operators".
- ^ See Hörmander 1990, p. 14, lemma 1.2.3.: the example is stated in implicit form by first defining

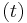 =exp
=exp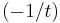 for
for  ∈ ℝ+, and then considering
∈ ℝ+, and then considering 
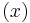 =
=
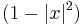 for x ∈ ℝn.
for x ∈ ℝn. - ^ See for example Hörmander 1990.
- ^ A proof of this fact can be found in Hörmander 1990, p. 25, Theorem 1.4.1.
References
- Friedrichs, Kurt Otto (January 1944), "The identity of weak and strong extensions of differential operators", Transactions of the American Mathematical Society 55 (1): 132–151, doi:10.1090/S0002-9947-1944-0009701-0, MR0009701, Zbl 0061.26201, http://www.ams.org/journals/tran/1944-055-00/S0002-9947-1944-0009701-0/home.html. The first paper where mollifiers where introduced.
- Friedrichs, Kurt Otto (1953), "On the differentiability of the solutions of linear elliptic differential equations", Communications on Pure and Applied Mathematics VI (3): 299–326, doi:10.1002/cpa.3160060301, MR0058828, Zbl 0051.32703, http://www3.interscience.wiley.com/journal/113395283/abstract. A paper where the differentiability of solutions of elliptic partial differential equations is investigated by using mollifiers.
- Friedrichs, Kurt Otto (1986), Morawetz, Cathleen S., ed., Selecta, Contemporary Mathematicians, Boston-Basel-Stuttgart: Birkhäuser Verlag, pp. 427 (Vol. 1); pp. 608 (Vol. 2), ISBN 0-8176-3270-0, Zbl 0613.01020, http://books.google.com/?id=l1Z_yHVjor4C&pg=PP1&dq=Kurt+Otto+Friedrichs+selecta. A selection from Friedrichs works with a biography and commentaries of David Isaacson, Fritz John, Tosio Kato, Peter Lax, Louis Nirenberg, Wolfgag Wasow, Harold Weitzner.
- Giusti, Enrico (1984), Minimal surfaces and functions of bounded variations, Monographs in Mathematics, 80, Basel-Boston-Stuttgart: Birkhäuser Verlag, pp. xii+240, ISBN 0-8176-3153-4 ISBN 3-7643-3153-4, MR0775682, Zbl 0545.49018, http://books.google.com/?id=dNgsmArDoeQC&printsec=frontcover&dq=Minimal+surfaces+and+functions+of+bounded+variations.
- Hörmander, Lars (1990), The analysis of linear partial differential operators I, Grundlehren der Mathematischen Wissenschaft, 256 (2nd ed.), Berlin-Heidelberg-New York: Springer-Verlag, ISBN 0-387-52343-X, ISBN 3-540-52343-X, MR1065136, Zbl 0712.35001.
- Sobolev, Sergei L. (1938), "Sur un théorème d'analyse fonctionnelle", Matematicheskiĭ Sbornik 4(46) (3): 471–497, Zbl 0022.14803, http://mi.mathnet.ru/eng/msb/v46/i3/p471 (in Russian, with French summary). The paper where Sergei Sobolev proved his embedding theorem, introducing and using integral operators very similar to mollifiers, without naming them.