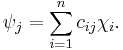Molecular orbital theory
In chemistry, molecular orbital (MO) theory is a method for determining molecular structure in which electrons are not assigned to individual bonds between atoms, but are treated as moving under the influence of the nuclei in the whole molecule.[1] In this theory, each molecule has a set of molecular orbitals, in which it is assumed that the molecular orbital wave function ψj may be written as a simple weighted sum of the n constituent atomic orbitals χi, according to the following equation:[2]
The cij coefficients may be determined numerically by substitution of this equation into the Schrödinger equation and application of the variational principle. This method is called the linear combination of atomic orbitals (LCAO) approximation and is used in computational chemistry. An additional unitary transformation can be applied on the system to accelerate the convergence in some computational schemes. Molecular orbital theory was seen as a competitor to valence bond theory in the 1930s, before it was realized that the two methods are closely related and that when extended they become equivalent.
Contents |
History
'Molecular orbital theory' was developed, in the years after valence bond theory had been established (1927), primarily through the efforts of Friedrich Hund, Robert Mulliken, John C. Slater, and John Lennard-Jones.[3] MO theory was originally called the Hund-Mulliken theory.[4] The word orbital was introduced by Mulliken in 1932.[4] By 1933, the molecular orbital theory had become accepted as a valid and useful theory.[5] According to German physicist and physical chemist Erich Hückel, the first quantitative use of molecular orbital theory was the 1929 paper of Lennard-Jones.[6] The first accurate calculation of a molecular orbital wavefunction was that made by Charles Coulson in 1938 on the hydrogen molecule.[7] By 1950, molecular orbitals were completely defined as eigenfunctions (wave functions) of the self-consistent field Hamiltonian and it was at this point that molecular orbital theory became fully rigorous and consistent.[8] This rigorous approach is known as the Hartree–Fock method for molecules although it had its origins in calculations on atoms. In calculations on molecules, the molecular orbitals are expanded in terms of an atomic orbital basis set, leading to the Roothaan equations.[9] This led to the development of many ab initio quantum chemistry methods. In parallel, molecular orbital theory was applied in a more approximate manner using some empirically derived parameters in methods now known as semi-empirical quantum chemistry methods.[10]
Overview
Molecular orbital (MO) theory uses a linear combination of atomic orbitals (LCAO) to represent molecular orbitals involving the whole molecule. These are often divided into bonding orbitals, anti-bonding orbitals, and non-bonding orbitals. A molecular orbital is merely a Schrödinger orbital that includes several, but often only two nuclei. If this orbital is of type in which the electron(s) in the orbital have a higher probability of being between nuclei than elsewhere, the orbital will be a bonding orbital, and will tend to hold the nuclei together. If the electrons tend to be present in a molecular orbital in which they spend more time elsewhere than between the nuclei, the orbital will function as an anti-bonding orbital and will actually weaken the bond. Electrons in non-bonding orbitals tend to be in deep orbitals (nearly atomic orbitals) associated almost entirely with one nucleus or the other, and thus they spend equal time between nuclei or not. These electrons neither contribute nor detract from bond strength.
Molecular orbitals are further divided according to the types of atomic orbitals combining to form a bond. These orbitals are results of electron-nucleus interactions that are caused by the fundamental force of electromagnetism. Chemical substances will form a bond if their orbitals become lower in energy when they interact with each other. Different chemical bonds are distinguished that differ by electron configuration (electron cloud shape) and by energy levels.
MO theory provides a global, delocalized perspective on chemical bonding. For example, in the MO theory for hypervalent molecules it is unnecessary to invoke a major role for d-orbitals, whereas valence bond theory normally uses hybridization with d-orbitals to explain hypervalency. In MO theory, any electron in a molecule may be found anywhere in the molecule, since quantum conditions allow electrons to travel under the influence of an arbitrarily large number of nuclei, as long as permitted by certain quantum rules. Although in MO theory some molecular orbitals may hold electrons that are more localized between specific pairs of molecular atoms, other orbitals may hold electrons that are spread more uniformly over the molecule. Thus, overall, bonding (and electrons) are far more delocalized (spread out) in MO theory, than is implied in valence bond (VB) theory. This makes MO theory more useful for the description of extended systems.
An example is that in the MO picture of benzene, composed of a hexagonal ring of 6 carbon atoms. In this molecule, 24 of the 30 total valence bonding electrons are located in 12 σ (sigma) bonding orbitals, which are located mostly between pairs of atoms (C-C or C-H), similar to the valence bond picture. However, in benzene the remaining 6 bonding electrons are located in 3 π (pi) molecular bonding orbitals that are delocalized around the ring. Two are in an MO, which has equal contributions from all 6 atoms. The other two orbitals have vertical nodes at right angles to each other. As in the VB theory, all of these 6 delocalized pi electrons reside in a larger space that exists above and below the ring plane. All carbon-carbon bonds in benzene are chemically equivalent. In MO theory this is a direct consequence of the fact that the 3 molecular pi orbitals form a combination that evenly spreads the extra 6 electrons over 6 carbon atoms.[11]
In molecules such as methane, the 8 valence electrons are found in 4 MOs that are spread out over all 5 atoms. However, it is possible to approximate the MOs with 4 localized orbitals similar in shape to sp3 hybrid orbitals predicted by VB theory. This is often adequate for σ (sigma) bonds, but it is not possible for the π (pi) orbitals. However, the delocalized MO picture is more appropriate for ionization and spectroscopic predictions. Upon ionization of methane, a single electron is taken from the MO, which surrounds the whole molecule, weakening all 4 bonds equally. VB theory would predict that one electron is removed for an sp3 orbital, resulting in the need for resonance between four valence bond structures, each of which with a one-electron bond.
As in benzene, in substances such as beta carotene, chlorophyll, or heme, some electrons the π (pi) orbitals are spread out in molecular orbitals over long distances in a molecule, giving rise to light absorption in lower energies (visible colors), a fact that is observed. This and other spectroscopic data for molecules are better explained in MO theory, with an emphasis on electronic states associated with multicenter orbitals, including mixing of orbitals premised on principles of orbital symmetry matching. The same MO principles also more naturally explain some electrical phenomena, such as high electrical conductivity in the planar direction of the hexagonal atomic sheets that exist in graphite. In MO theory, "resonance" (a mixing and blending of VB bond states) is a natural consequence of symmetry. For example, in graphite, as in benzene, it is not necessary to invoke the sp2 hybridization and resonance of VB theory, in order to explain electrical conduction. Instead, MO theory simply recognizes that some electrons in the graphite atomic sheets are completely delocalized over arbitrary distances, and reside in very large molecular orbitals that cover an entire graphite sheet, and some electrons are thus as free to move and conduct electricity in the sheet plane, as if they resided in a metal.
See also
References
- ^ Daintith, J. (2004). Oxford Dictionary of Chemistry. New York: Oxford University Press. ISBN 0-19-860918-3.
- ^ Licker, Mark, J. (2004). McGraw-Hill Concise Encyclopedia of Chemistry. New York: McGraw-Hill. ISBN 0-07-143953-6.
- ^ Coulson, Charles, A. (1952). Valence. Oxford at the Clarendon Press.
- ^ a b Spectroscopy, Molecular Orbitals, and Chemical Bonding - Robert Mulliken's 1966 Nobel Lecture
- ^ Lennard-Jones Paper of 1929 - Foundations of Molecular Orbital Theory.
- ^ Hückel, E. (1934). Trans. Faraday Soc. 30, 59.
- ^ Coulson, C.A. (1938). Proc. Camb. Phil. Soc. 34, 204.
- ^ Hall, G.G. Lennard-Jones, Sir John. (1950). Proc. Roy. Soc. A202, 155.
- ^ Frank Jensen, Introduction to Computational Chemistry, John Wiley and Sons, 1999, pg 65 - 69, ISBN 0 471 98055
- ^ Frank Jensen, Introduction to Computational Chemistry, John Wiley and Sons, 1999, pg 81 - 92, ISBN 0 471 98055
- ^ Introduction to Molecular Orbital Theory - Imperial College London
External links
- Molecular Orbital Theory - Purdue University
- Molecular Orbital Theory - Sparknotes
- Molecular Orbital Theory - Mark Bishop's Chemistry Site
- Introduction to MO Theory - Queen Mary, London University
- Molecular Orbital Theory - a related terms table