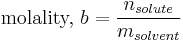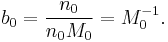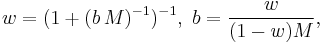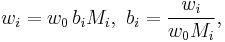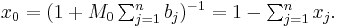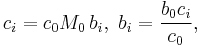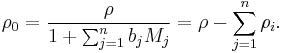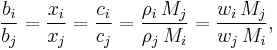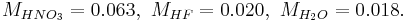Molality

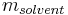In chemistry, the molality, b (or m), of a solvent/solute combination is defined as the amount of solute, $n_{solute}$ , divided by the mass of the solvent, $m_{solvent}$ (not the mass of the solution):^[1]

$\text{molality, }b = \frac{n_{solute}}{m_{solvent}}$

If a mixture contains more than one solute or solvent, each solvent/solute combination in the mixture is defined in this same way.

1 Origin
2 Unit
3 Example
4 Usage considerations
5 Relation to other compositional properties
6 References

Origin

The earliest such definition of the intensive property molality and of its adjectival unit, the now-deprecated molal (formerly, a variant of molar, describing a solution of unit molar concentration), appear to have been coined by G. N. Lewis and M. Randall in their 1923 publication of Thermodynamics and the Free Energies of Chemical Substances.^[2] Though the two words are subject to being confused with one another, the molality and molarity of a weak aqueous solution happen to be nearly the same, as one kilogram of water (the solvent) occupies 1 liter of volume at room temperature and the small amount of solute would have little effect on the volume.

Unit

The SI unit for molality is mol/kg.

A solution with a molality of 3 mol/kg is often described as "3 molal" or "3 m". However, following the SI system of units, the National Institute of Standards and Technology, the United States authority on measurement, considers the term "molal" and the unit symbol "m" to be obsolete, and suggests mol/kg or a related unit of the SI.^[3] This recommendation has not been universally implemented in academia yet.

Example

Dissolving 1.0 mol of table salt (NaCl) in 2.0 kg of water constitutes a solution with a molality of m(NaCl) = 0.50 mol/kg. Adding and dissolving sugar to the solution does not change the molality of NaCl.

Usage considerations

Advantages:

Compared to molar concentration or mass concentration, the preparation of a solution of a given molality requires only a good scale: both solvent and solute need to be weighed, as opposed to measured volumetrically, which would be subject to variations in density due to the ambient conditions of temperature and pressure; this is an advantage because, in chemical compositions, the mass, or the amount, of a pure known substance is more relevant than its volume: a contained measured amount of substance may change in volume with ambient conditions, but its amount and mass are unvarying, and chemical reactions occur in proportions of mass, not volume. The mass-based nature of molality implies that it can be readily converted into a mass ratio (or mass fraction, "w," ratio),

$b\,M_{solute}=\frac{m_{solute}}{m_{solvent}}=\frac{w_{solute}}{w_{solvent}},$

where the symbol M stands for molar mass, or into a mole ratio (or mole fraction, "x," ratio)

$b\,M_{solvent}=\frac{n_{solute}}{n_{solvent}}=\frac{x_{solute}}{x_{solvent}}.$

The advantage of molality over other mass-based fractions is the fact that the molality of one solute in a single-solvent solution is independent of the presence or absence of other solutes.

Problem areas:

Unlike all the other compositional properties listed in "Relation" section (below), molality depends on our choice of the substance we call “solvent” in an arbitrary mixture. If there is only one pure liquid substance in a mixture, the choice is clear, but not all solutions are this clear-cut: in an alcohol-water solution, either one could be called the solvent; in an alloy, or solid solution, there is no clear choice and all constituents may be treated alike. In such situations, mass or mole fraction is the preferred compositional specification.

Relation to other compositional properties

In what follows, the solvent may be given the same treatment as the other constituents of the solution, such that the molality of the solvent of an n-solute solution, say b₀, is found to be nothing more than the reciprocal of its molar mass, M₀:

$b_0=\frac{{n_0}}{{n_0 M_0}}=M_0^{-1}.$

Mass fraction

The conversions to and from the mass fraction, $w$ , of the solute in a single-solute solution are

$w=(1%2B(b\,M)^{-1})^{-1},\ b=\frac{w}{(1-w)M} ,$

where b is the molality and M is the molar mass of the solute.

More generally, for an n-solute/one-solvent solution, letting b_i and w_i be, respectively, the molality and mass fraction of the i-th solute,

$w_i=w_0\,b_i M_i,\ b_i=\frac{w_i}{w_0 M_i},$

where M_i is the molar mass of the i-th solute, and w₀ is the mass fraction of the solvent, which is expressible both as a function of the molalities as well as a function of the other mass fractions,

$w_0=(1%2B\textstyle\sum_{j=1}^{n}{b_j M_j})^{-1}=1-\sum_{j=1}^{n}{w_j}.$

Mole fraction

The conversions to and from the mole fraction, x, of the solute in a single-solute solution are

$x=(1%2B(M_0\,b)^{-1})^{-1},\ b=\frac{x}{M_0(1-x)},$

where M₀ is the molar mass of the solvent.

More generally, for an n-solute/one-solvent solution, letting x_i be the mole fraction of the i-th solute,

$x_i=x_0 M_0\,b_i,\ b_i=\frac{b_0 x_i}{x_0},$

where x₀ is the mole fraction of the solvent, expressible both as a function of the molalities as well as a function of the other mole fractions:

$x_0=(1%2BM_0\textstyle \sum_{j=1}^{n}{b_j})^{-1}=1-\sum_{j=1}^{n}{x_j}.$

Molar concentration (Molarity)

The conversions to and from the molar concentration, c, for one-solute solutions are

$c = \frac{\rho\, b}{1%2B b M},\ b=\frac{c}{\rho-cM},$

where ρ is the mass density of the solution, b is the molality, and M is the molar mass of the solute.

For solutions with n solutes, the conversions are

$c_i =c_0 M_0\,b_i,\ b_i=\frac{b_0 c_i}{c_0},$

where the molar concentration of the solvent c₀ is expressible both as a function of the molalities as well as a function of the molarities:

$c_0=\frac{\rho\,b_0}{1%2B \sum_{j=1}^{n}{b_j M_j}}=\frac{\rho-\sum_{j=1}^{n}{c_i M_i}}{M_0}.$

Mass concentration

The conversions to and from the mass concentration, ρ_solute, of an single-solute solution are

$\rho_{solute} = \frac{\rho\,b\,M}{1%2Bb M},\ b=\frac{\rho_{solute}}{M (\rho-\rho_{solute})},$

where ρ is the mass density of the solution, b is the molality, and M is the molar mass of the solute.

For the general n-solute solution, the mass concentration of the i-th solute, ρ_i, is related to its molality, b_i, as follows:

$\rho_i = \rho_0\,b_i M_i,\ b_i=\frac{\rho_i}{\rho_0 M_i},$

where the mass concentration of the solvent, ρ₀, is expressible both as a function of the molalities as well as a function of the mass concentrations:

$\rho_0=\frac{\rho}{1%2B\sum_{j=1}^n b_j M_j}=\rho-\sum_{j=1}^{n}{\rho_i}.$

Equal ratios

Alternatively, we may use just the last two equations given for the compositional property of the solvent in each of the preceding sections, together with the relationships given below, to derive the remainder of properties in that set:

$\frac{b_i}{b_j}=\frac{x_i}{x_j}=\frac{c_i}{c_j}=\frac{\rho_i\,M_j}{\rho_j\,M_i}=\frac{w_i\,M_j}{w_j\,M_i},$

where i and j are subscripts representing all the constituents, the n solutes plus the solvent.

Example of conversion

An acid mixture consists of 0.76/0.04/0.20 mass fractions of (70% HNO₃)/(49% HF)/(H₂O), where the percentages refer to mass fractions of the bottled acids carrying a balance of H₂O. The first step is determining the mass fractions of the constituents:

$\begin{align} w_{HNO_3}&=0.70\times 0.76=0.532\\ w_{HF}&=0.49\times 0.04=0.0196\\ w_{H_2O}&=1-w_{HNO_3}-w_{HF}=0.448\\ \end{align}$

The approximate molar masses in kg/mol are

$M_{HNO_3}=0.063,\ M_{HF}=0.020,\ M_{H_2O}=0.018.$

First derive the molality of the solvent, in mol/kg,

$b_{H_2O}=(M_{H_2O})^{-1}=1/0.018,$

and use that to derive all the others by use of the equal ratios:

$\frac{b_{HNO_3}}{b_{H_2O}}=\frac{w_{HNO_3}M_{H_2O}}{w_{H_2O}M_{HNO_3}} \ \therefore b_{HNO_3}=18.83.$

Actually, b_H₂O cancels out, because it is not needed. In this case, there is a more direct equation: we use it to derive the molality of HF:

$b_{HF}=\frac{w_{HF}}{w_{H_2O}M_{HF}}=2.19.$

The mole fractions may be derived from this result:

$\begin{align} &x_{H_2O}=(1%2BM_{H_2O}(b_{HNO_3}%2Bb_{HF}))^{-1}=0.726,\\ &\frac{x_{HNO_3}}{x_{H_2O}}=\frac{b_{HNO_3}}{b_{H_2O}}\ \therefore x_{HNO_3}=0.246,\\ &x_{HF}=1-x_{HNO_3}-x_{H_2O}=0.029. \end{align}$

References

^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "molality".
^ www.OED.com. Oxford University Press. 2011.
^ "NIST Guide to SI Units". http://physics.nist.gov/Pubs/SP811/sec11.html. Retrieved 2007-12-17.

Articles related to solutions

Solution	Ideal solution · Aqueous solution · Solid solution · Buffer solution · Flory-Huggins · Mixture · Suspension · Colloid · Phase diagram · Eutectic point · Alloy · Saturation · Supersaturation · Serial dilution · Dilution (equation) · Apparent molar property

Concentration and related quantities	Molar concentration · Mass concentration · Number concentration · Volume concentration · Normality · Percentage solution · Molality · Mole fraction · Mass fraction · Mixing ratio

Solubility	Solubility equilibrium · Total dissolved solids · Solvation · Solvation shell · Enthalpy of solution · Lattice energy · Raoult's law · Henry's law · Solubility table (data) · Solubility chart

Solvent	(category) · Acid dissociation constant · Protic solvent · Inorganic nonaqueous solvent · Solvation · List of boiling and freezing information of solvents Partition coefficient · Polarity · Hydrophobe · Hydrophile · Lipophilic · Amphiphile