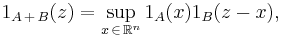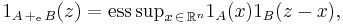Minkowski addition
In geometry, the Minkowski sum (also known as dilation) of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e. the set
Contents |
Example
For example, if we have two 2-simplices (triangles), with points represented by
- A = {(1, 0), (0, 1), (0, −1)}
and
- B = {(0, 0), (1, 1), (1, −1)},
then the Minkowski sum is
- A + B = {(1, 0), (2, 1), (2, −1), (0, 1), (1, 2), (1, 0), (0, −1), (1, 0), (1, −2)}, which looks like a hexagon, with three 'repeated' points at (1, 0).
For Minkowski addition, the zero set, {0}, containing only the zero vector, 0, has special importance: For every non-empty subset, S, of a vector space
- S + {0} = S;
in algebraic terminology, the zero set, {0}, is the identity element of Minkowski addition (on the collection of non-empty sets).[1]
Convex hulls of Minkowski sums
In a real vector space, a non-empty set Q is defined to be convex if, for each pair of its points, every point on the line segment that joins them is a subset of Q. For example, a solid disk, ●, is convex but a circle, ○, is not, because it does not contain a line segment joining its points, ∅; the non-convex set of three integers, {0, 1, 2}, is contained in the interval, [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent shape, is non-convex. The empty set is convex, either by definition[2] or vacuously, depending on the author.
More formally, a set, Q, is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval, [0, 1], the point
- (1 − λ) v0 + λv1
is a member of Q.
By mathematical induction, a set, Q, is convex if and only if every convex combination of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, …, vD} of a vector space is any weighted average, λ0v0 + λ1v1 + … + λDvD, for some indexed set of non-negative real numbers, {λd}, satisfying the equation λ0 + λ1 + … + λD = 1.[3]
The definition of a convex set implies that the intersection of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.[2]
Minkowski addition behaves well with respect to the operation of taking convex hulls, as shown by the following proposition:
- For all subsets S1 and S2 of a real vector-space, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls
- Conv(S1 + S2) = Conv(S1) + Conv(S2).
This result holds more generally for each finite collection of non-empty sets
- Conv(∑Sn) = ∑Conv(Sn).
In mathematical terminology, the operations of Minkowski summation and of forming convex hulls are commuting operations.[4][5]
Essential Minkowski sum
There is also a notion of the essential Minkowski sum +e of two subsets of Euclidean space. Note that the usual Minkowski sum can be written as
Thus, the essential Minkowski sum is defined by
where μ denotes n-dimensional Lebesgue measure. The reason for the term "essential" is the following property of indicator functions: while
it can be seen that
where "ess sup" denotes the essential supremum.
Applications
Minkowski addition plays a central role in mathematical morphology. It arises in the brush-and-stroke paradigm of 2D computer graphics (with various uses, notably by Donald E. Knuth in Metafont), and as the solid sweep operation of 3D computer graphics.
Motion planning
Minkowski sums are used in motion planning of an object among obstacles. They are used for the computation of the configuration space, which is the set of all admissible positions of the object. In the simple model of translational motion of an object in the plane, where the position of an object may be uniquely specified by the position of a fixed point of this object, the configuration space are the Minkowski sum of the set of obstacles and the movable object placed at the origin and rotated 180 degrees.
Numerical control (NC) machining
In numerical control machining, the programming of the NC tool exploits the fact that the Minkowski sum of the cutting piece with its trajectory gives the shape of the cut in the material.
Algorithms for computing Minkowski sums
Planar case
Two convex polygons in the plane
For two convex polygons P and Q in the plane with m and n vertices, their Minkowski sum is a convex polygon with at most m + n vertices and may be computed in time O (m + n) by a very simple procedure, which may be informally described as follows. Assume that the edges of a polygon are given and the direction, say, counterclockwise, along the polygon boundary. Then it is easily seen that these edges of the convex polygon are ordered by polar angle. Let us merge the ordered sequences of the directed edges from P and Q into a single ordered sequence S. Imagine that these edges are solid arrows which can be moved freely while keeping them parallel to their original direction. Assemble these arrows in the order of the sequence S by attaching the tail of the next arrow to the head of the previous arrow. It turns out that the resulting polygonal chain will in fact be a convex polygon which is the Minkowski sum of P and Q.
Other
If one polygon is convex and another one is not, the complexity of their Minkowski sum is O(nm). If both of them are nonconvex, their Minkowski sum complexity is O((mn)2).
See also
Notes
- ^ The empty set is important in Minkowski addition, because the empty set annihilates every other subset: for every subset, S, of a vector space, its sum with the empty set is empty: S + ∅ = ∅.
- ^ a b Rockafellar (1997, p. 10)
- ^ Arrow & Hahn (1980, p. 376). Rockafellar (1997, pp. 10–11). Green & Heller (1981, p. 37)
- ^ Theorem 3 (pages 562–563): Krein, M.; Šmulian, V. (1940). "On regularly convex sets in the space conjugate to a Banach space". Annals of Mathematics (2), Second series 41: pp. 556–583. doi:10.2307/1968735. JSTOR 1968735. MR2009.
- ^ For the commutativity of Minkowski addition and convexification, see Theorem 1.1.2 (pages 2–3) in Schneider; this reference discusses much of the literature on the convex hulls of Minkowski sumsets in its "Chapter 3 Minkowski addition" (pages 126–196): Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. pp. xiv+490. ISBN 0-521-35220-7. MR1216521.
References
- Arrow, Kenneth J.; Hahn, Frank H. (1980). General competitive analysis. Advanced textbooks in economics. 12 (reprint of (1971) San Francisco, CA: Holden-Day, Inc. Mathematical economics texts. 6 ed.). Amsterdam: North-Holland. ISBN 0-444-85497-5. MR439057.
- Gardner, Richard J. (2002), "The Brunn-Minkowski inequality", Bull. Amer. Math. Soc. (N.S.) 39 (3): 355–405 (electronic), doi:10.1090/S0273-0979-02-00941-2
- Green, Jerry; Heller, Walter P. (1981). "1 Mathematical analysis and convexity with applications to economics". In Arrow, Kenneth Joseph; Intriligator, Michael D. Handbook of mathematical economics, Volume I. Handbooks in economics. 1. Amsterdam: North-Holland Publishing Co. pp. 15–52. doi:10.1016/S1573-4382(81)01005-9. ISBN 0-444-86126-2. MR634800. http://www.sciencedirect.com/science/article/B7P5Y-4FDF0FN-5/2/613440787037f7f62d65a05172503737.
- Henry Mann (1976), Addition Theorems: The Addition Theorems of Group Theory and Number Theory (Corrected reprint of 1965 Wiley ed.), Huntington, New York: Robert E. Krieger Publishing Company, ISBN 0882754181
- Rockafellar, R. Tyrrell (1997). Convex analysis. Princeton landmarks in mathematics (Reprint of the 1979 Princeton mathematical series 28 ed.). Princeton, NJ: Princeton University Press. pp. xviii+451. ISBN 0-691-01586-4. MR1451876. MR274683.
- Nathanson, Melvyn B. (1996), Additive Number Theory: Inverse Problems and Geometry of Sumsets, GTM, 165, Springer, Zbl 0859.11003.
- Oks, Eduard; Sharir, Micha (2006), "Minkowski Sums of Monotone and General Simple Polygons", Discrete and Computational Geometry 35 (2): 223–240, doi:10.1007/s00454-005-1206-y.
- Schneider, Rolf (1993), Convex bodies: the Brunn-Minkowski theory, Cambridge: Cambridge University Press.
- Tao, Terence & Vu, Van (2006), Additive Combinatorics, Cambridge University Press.
External links
- Howe, Roger (1979), On the tendency toward convexity of the vector sum of sets, Cowles Foundation discussion papers, 538, Cowles Foundation for Research in Economics, Yale University, http://econpapers.repec.org/RePEc:cwl:cwldpp:538
- Minkowski Sums, in Computational Geometry Algorithms Library
- The Minkowski Sum of Two Triangles and The Minkowski Sum of a Disk and a Polygon by George Beck, The Wolfram Demonstrations Project.
- Minkowski's addition of convex shapes by Alexander Bogomolny: an applet
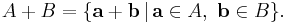
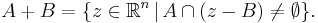
![A %2B_{\mathrm{e}} B = \{ z \in \mathbb{R}^{n} \,|\, \mu \left[A \cap (z - B)\right] > 0 \},](/2012-wikipedia_en_all_nopic_01_2012/I/b9171c19ff261c7262c371a806393df6.png)