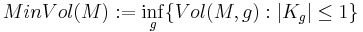Minimal volume
In mathematics, in particular in differential geometry, the minimal volume is a number that describes one aspect of a Riemannian manifold's topology. This invariant was introduced by Mikhail Gromov.
Contents |
Definition
Consider a closed orientable connected smooth manifold 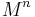 with a smooth Riemannian metric
with a smooth Riemannian metric  , and define
, and define 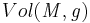 to be the volume of a manifold
to be the volume of a manifold  with the metric
with the metric  . Let
. Let  represent the sectional curvature.
represent the sectional curvature.
The minimal volume of  is a smooth invariant defined as
is a smooth invariant defined as
that is, the infimum of the volume of  over all metrics with bounded sectional curvature.
over all metrics with bounded sectional curvature.
Clearly, any manifold  may be given an arbitrarily small volume by selecting a Riemannian metric
may be given an arbitrarily small volume by selecting a Riemannian metric  and scaling it down to
and scaling it down to 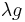 , as
, as 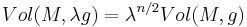 . For a meaningful definition of minimal volume, it is thus necessary to prevent such scaling. The inclusion of bounds on sectional curvature suffices, as
. For a meaningful definition of minimal volume, it is thus necessary to prevent such scaling. The inclusion of bounds on sectional curvature suffices, as 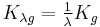 . If
. If 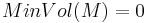 , then
, then 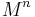 can be "collapsed" to a manifold of lower dimension (and thus one with
can be "collapsed" to a manifold of lower dimension (and thus one with  -dimensional volume zero) by a series of appropriate metrics; this manifold may be considered the Hausdorff limit of the related sequence, and the bounds on sectional curvature ensure that this convergence takes place in a topologically meaningful fashion.
-dimensional volume zero) by a series of appropriate metrics; this manifold may be considered the Hausdorff limit of the related sequence, and the bounds on sectional curvature ensure that this convergence takes place in a topologically meaningful fashion.
Related topological invariants
The minimal volume invariant is connected to other topological invariants in a fundamental way; via Chern-Weil theory, there are many topological invariants which can be described by integrating polynomials in the curvature over  . In particular, the Chern classes and Pontryagin classes are bounded above by the minimal volume.
. In particular, the Chern classes and Pontryagin classes are bounded above by the minimal volume.
Properties
Gromov has conjectured that every closed simply connected odd-dimensional manifold has zero minimal volume. This conjecture clearly does not hold for even-dimensional manifolds.
References
- Gromov, M. Metric Structures for Riemannian and Non-Riemannian Spaces, Birkhäuser (1999) ISBN 0-8176-3898-9.
- Gromov, M. Volume and bounded cohomology, Publ. Math. IHES 56 (1982) 1—99.